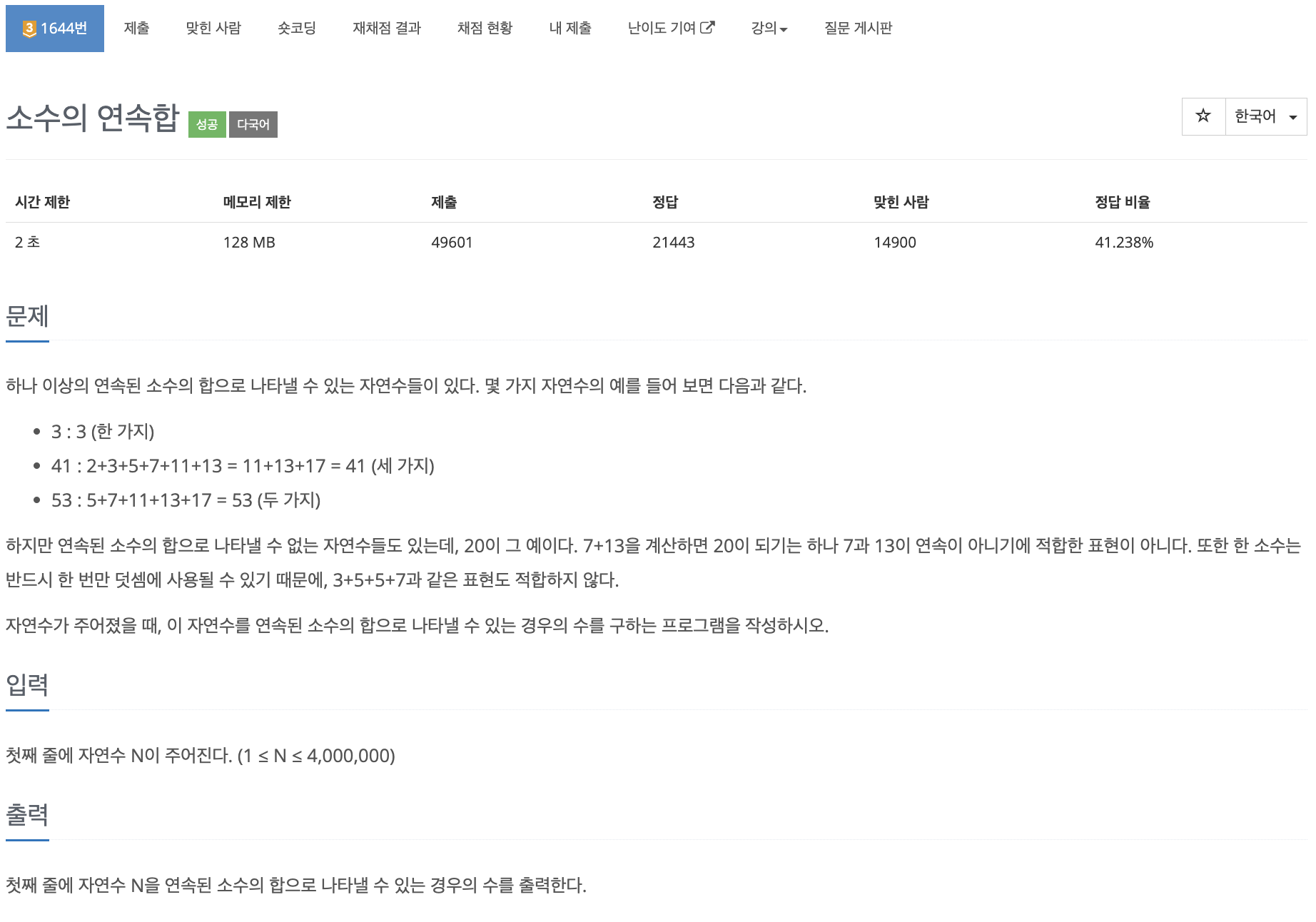
BOJ 백준 1644번 소수의 연속합 | Python, Java
🔎 문제 설명
💛 골드 3
- 난이도 ★☆☆☆ - 투포인터 - 에라토스테네스의 체
문제 풀이
- 소수 배열 구하기
- 특정 수가 되는 소수 연속합 개수 구하기
💡 에라토스테네스의 체
소수를 구하는 건 사실 소수의 개념만 알고 있다면 너무 쉬운 문제다. 그러나 이 문제에서는 일반적인 방법으로는 시간초과 를 면할 수 없기 때문에 에라토스테네스의 체로 문제에 접근해야 한다.
📌 에라토스테네스의 체가 뭔데?
이번에 처음 알게 된 에라토스테네스의 체에 관한 설명은 아래에 간단하게 정리하고자 한다. 이걸로만 풀리는 문제가 있다고 하니 알아두면 좋을 것 같다!
다시 돌아와서 이렇게 에라토스테네스의 체로 소수 배열을 구했다면, 연속합이 특정 수가 되는 횟수를 구할 땐 투포인터를 사용하였다. 연속합 문제 유형은 투포인터를 이용하면 비교적 빠르게 계산할 수 있다. 코드는 바로 아래 첨부하였다.
💻 내 코드
Python 버전
import sys
input = sys.stdin.readline
N = int(input())
prime_test = [False,False] + [True] * (N-1)
primes = []
for i in range(N+1):
if prime_test[i]:
for j in range(2*i, N+1, i):
if prime_test[j]:
prime_test[j] = False
primes.append(i)
answer = 0
total = 0
end = 0
for start in range(len(primes)):
while total < N and end < len(primes):
total += primes[end]
end += 1
if total == N:
answer += 1
total -= primes[start]
print(answer)
Java 버전
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
Boolean[] isPrimes = new Boolean[N+1];
List<Integer> primes = new ArrayList<>();
Arrays.fill(isPrimes, true);
isPrimes[1] = false;
int answer = 0;
for (int i=2;i*i<=N;i++){
if (isPrimes[i]) {
for (int j=2*i;j<=N;j+=i) {
isPrimes[j] = false;
}
}
}
for (int i=2;i<=N;i++){
if (isPrimes[i]) primes.add(i);
}
int tempTotal = 0;
int end = 0;
for (int start=0;start<primes.size();start++) {
while (tempTotal < N && end < primes.size()) {
tempTotal += primes.get(end++);
}
if (tempTotal == N) answer ++;
tempTotal -= primes.get(start);
}
System.out.println(answer);
}
}
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).