BOJ 백준 17069번 파이프 옮기기 2 | Java
🔎 문제 설명
💛 Gold 4
- 난이도 ★★☆☆ - DP
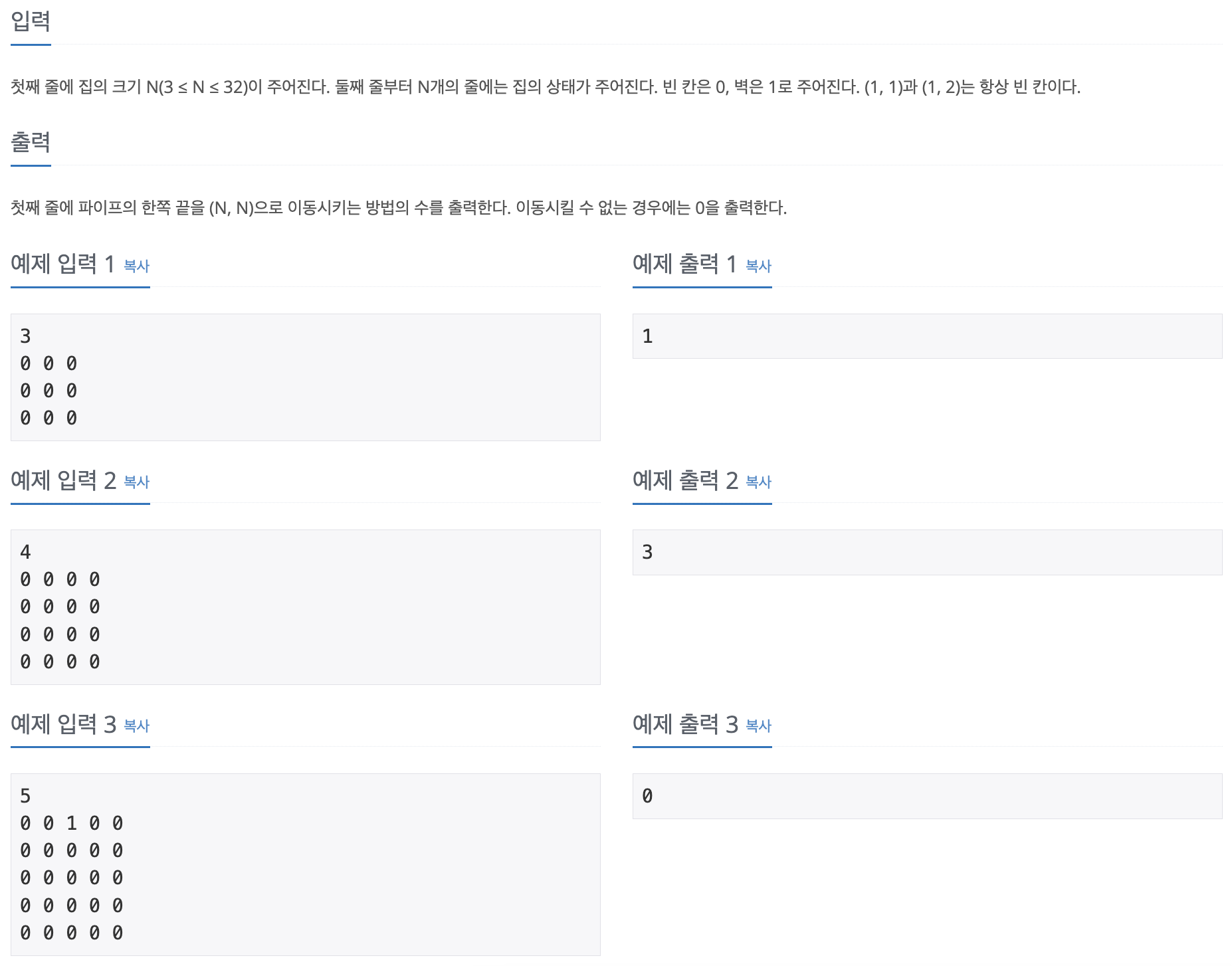
바로 이전에 풀어본 📌 백준 파이프 옮기기1 문제와 거의 동일한 문제였다. 차이점이 있다면 N의 범위가 2배로 늘어났다는 점!
[ O(3^{N*N}) ]
시간복잡도가 위와 같기 때문에 파이프옮기기1은 DFS로 풀렸지만 파이프옮기기2는 DFS로 풀면 시간초과가 난다. 이를 극복하기 위해서 생각한 게 바로 ➡️ DP 동적 계획법!
생각한 틀은 다음과 같다.
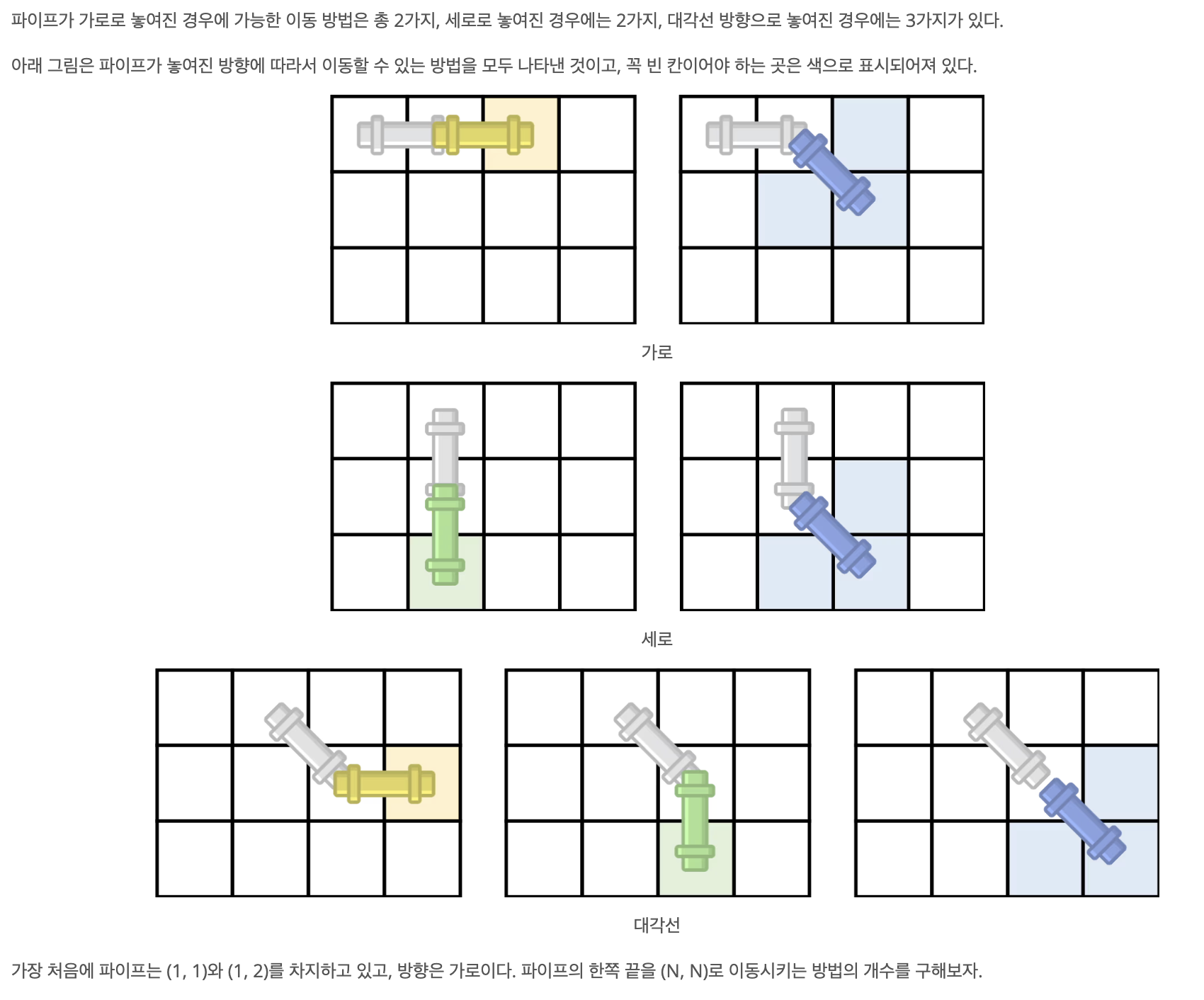
- 현재 대각선 방향이 되기 위해서는 이전 방향이 가로, 세로, 대각선일 수 있음
- 현재 가로 방향이 되기 위해서는 이전 방향이 가로, 대각선일 수 있음
- 현재 세로 방향이 되기 위해서는 이전 방향이 세로, 대각선일 수 있음
- 3차원 DP 배열을 만들자! N x N x 3(방향)
이밖에도 벽을 만나는 경우는 DP 배열값은 0으로, 가로/세로/대각선 방향이 모두 확보되지 않으면 대각선 방향이 성립될 수 없다는 점을 고려하면서 코드를 짰다. 코드는 아래에 첨부하였다.
아 그리고! 로직이 동일한데 틀린다 하는 사람은 데이터 타입을 long으로 바꿔서 제출해보자.
💻 내 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/*
메모리 14880 kb
실행시간 284 ms
*/
public class Main {
static int N, board[][];
static long answer, dp[][][];
static int[] dx = {0,1,1};
static int[] dy = {1,0,1};
static StringTokenizer st;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
board = new int[N+1][N+1];
dp = new long[N+1][N+1][3];
answer = 0;
for (int i=1;i<N+1;i++) {
st = new StringTokenizer(br.readLine());
for (int j=1;j<N+1;j++) {
board[i][j] = Integer.parseInt(st.nextToken());
}
}
dp[1][2][0] = 1;
for (int i=1; i<N+1; i++) {
for (int j=3; j<N+1; j++){
if (board[i][j]==1) continue;
dp[i][j][0] = dp[i][j-1][0]+dp[i][j-1][2];
dp[i][j][1] = dp[i-1][j][1]+dp[i-1][j][2];
// 대각선 방향으로 갈 수 있는지 체크
if (board[i-1][j]!=0 || board[i][j-1]!=0) continue;
dp[i][j][2] = dp[i-1][j-1][0]+dp[i-1][j-1][1]+dp[i-1][j-1][2];
}
}
answer = dp[N][N][0]+dp[N][N][1]+dp[N][N][2];
System.out.println(answer);
}
}
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).