BOJ 백준 23801번 두 단계 최단 경로 2 | Java
🔎 문제 설명
💛 Gold 3
- 난이도 ★★★☆ - Dijkstra 다익스트라
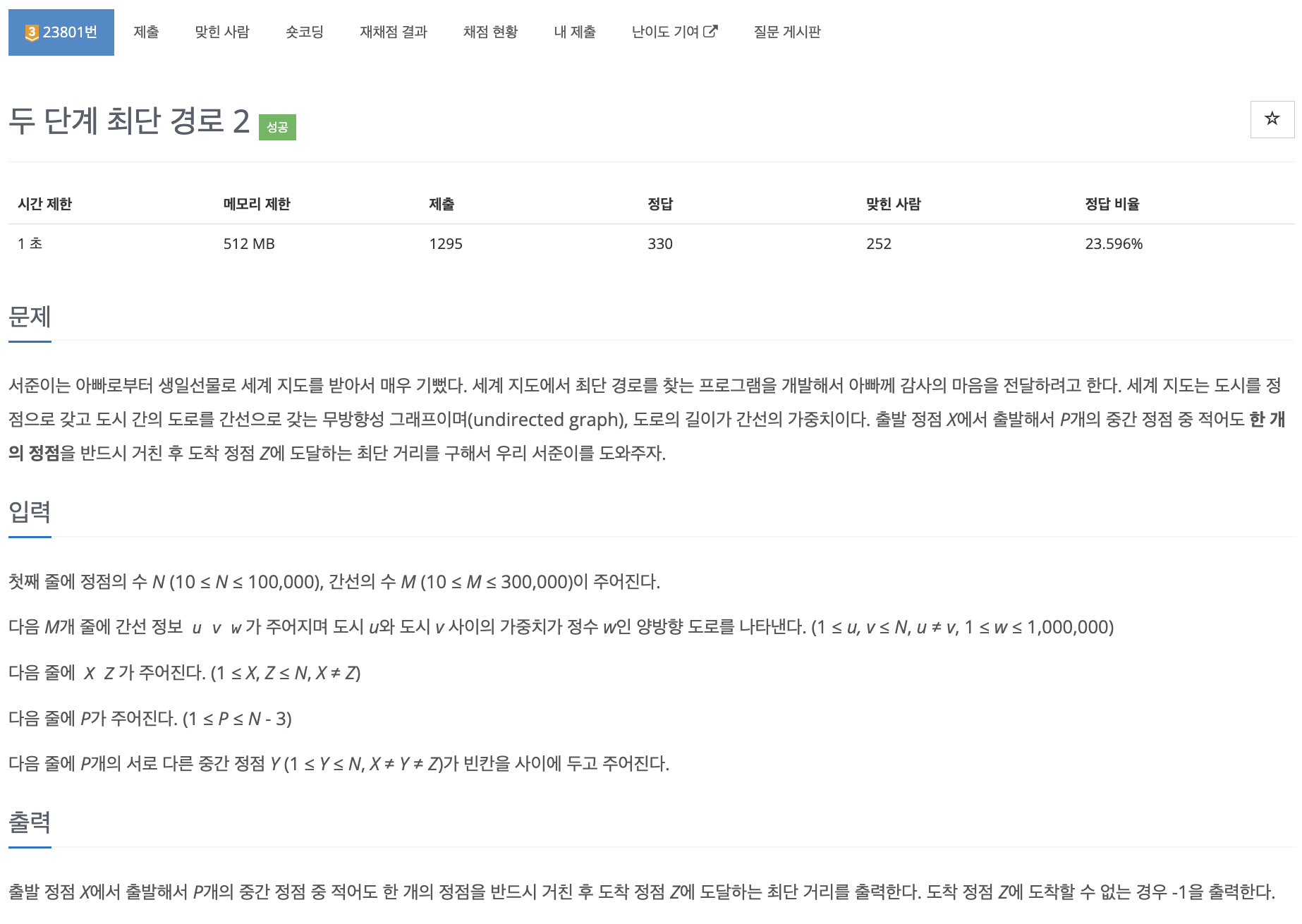
문제 제한사항을 보면 시간 복잡도에 주의해야겠다는 생각이 들어야 한다.
일단 최단경로 문제이고, 양의 가중치를 가지고 있다는 점에서 DFS나 다익스트라를 떠올릴 수 있다. DFS는 시간 제한 1초에 무조건 걸리기 때문에 다익스트라로 시도했다. 그리고 이걸로 거쳤던 시행착오를 하나씩 정리하고자 한다. (정답 코드는 맨 아래에 첨부해놓았다)
📍 핵심
중간 정점이 주어지고 그 중 적어도 한 개의 정점을 반드시 거쳐야 한다.
생각해보면 정점 mid 에서부터 시작점까지, 정점 mid 에서부터 도착점까지의 최단 거리를 구해 이들을 더해준 값이 해당 정점 mid 을 지나는 최종 최단 거리가 된다.
❌ Approach 1: 시간초과
그래서 처음엔 정점을 for문으로 돌리면서 그때마다 시작점으로 다익스트라 1회, 도착점으로 다익스트라 1회해서 답을 찾고자 했다.
for (int m : mids) {
answer = Math.min(answer, findShortest(m, x)+findShortest(m, z));
}
그래서 위와 같이 시도했더니 시간초과가 발생!
❓ 왜 시간초과가 났을까?
다익스트라의 시간복잡도 $O(ElogE)$
이 문제에서 간선과 중점 개수는 약 30만 개까지 주어질 수 있고 다익스트라의 시간복잡도는 ElogE 이니까 실행시간은 30만 x 30만 x log(30만) * 2 => 900,000,000 * 5 * 2 까지도 걸릴 수 있다는 말이다! 보통 1억을 1초로 보기 때문에 터무니 없이 시간 초과에 걸린다는 것을 알 수 있지… 아래 코드는 시간초과가 났던 전체 코드이다.
import java.io.*;
import java.util.*;
public class Main {
final static int INF = Integer.MAX_VALUE;
static int N, M, answer;
static class Edge implements Comparable<Edge> {
int to, weight;
public Edge(int to, int weight) {
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.weight, o.weight);
}
}
static ArrayList<Edge> edges[];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
edges = new ArrayList[N+1];
answer = INF;
for (int i=1; i<N+1; i++) {
edges[i] = new ArrayList<>();
}
for (int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edges[from].add(new Edge(to, weight));
edges[to].add(new Edge(from, weight));
}
int x, z;
st = new StringTokenizer(br.readLine());
x = Integer.parseInt(st.nextToken());
z = Integer.parseInt(st.nextToken());
int P = Integer.parseInt(br.readLine());
int mids[] = new int[P];
mids = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
for (int m : mids) {
answer = Math.min(answer, findShortest(m, x)+findShortest(m, z));
}
System.out.println(answer);
}
// dijkstra
private static int findShortest(int start, int end) {
boolean[] visited = new boolean[N+1];
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(start, 0));
visited[start] = true;
int[] minDist = new int[N+1];
Arrays.fill(minDist, INF);
minDist[start] = 0;
while (!pq.isEmpty()) {
Edge now = pq.poll();
visited[now.to] = true;
if (now.to==end) return minDist[end];
for (Edge e: edges[now.to]) {
if (visited[e.to]) continue;
if (minDist[e.to] > minDist[now.to] + e.weight) {
minDist[e.to] = e.weight + minDist[now.to];
pq.add(new Edge(e.to, minDist[e.to]));
}
}
}
return -1;
}
}
⭕️ Approach 2: 정답
첫 번째 풀이에 불필요하게 다익스트라를 많이 호출한다는 걸 알았다면 그게 맞습니다!
생각해보면 무방향 간선 그래프이기 때문에 시작점에서부터 다익스트라를 돌리면 나머지 정점에서 시작점까지의 최단 거리가 이미 구해진 거라 정점마다 다익스트라를 돌릴 필요가 없다.
Memoization
다익스트라는 처음에만 시작점에서 1번, 도착점에서 1번 돌리고 저장해놓으면 정점마다 돌릴 필요 없이 저장된 값을 가져오면 된다.
findShortest(x, minDist1);
findShortest(z, minDist2);
for (int m : mids) {
if (minDist1[m]!=INF && minDist2[m]!=INF)
answer = Math.min(answer, minDist1[m]+minDist2[m]);
}
전체 코드는 아래에 첨부해놓았다!
💻 내 코드 (정답)
import java.io.*;
import java.util.*;
public class Main_23801_G3_두_단계_최단_경로_2 {
final static long INF = Long.MAX_VALUE;
static int N, M;
static long answer;
static long[] minDist1, minDist2;
static class Edge implements Comparable<Edge> {
int to;
long weight;
public Edge(int to, long weight) {
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return Long.compare(this.weight, o.weight);
}
}
static ArrayList<Edge> edges[];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
edges = new ArrayList[N+1];
answer = INF;
for (int i=1; i<N+1; i++) {
edges[i] = new ArrayList<>();
}
for (int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edges[from].add(new Edge(to, weight));
edges[to].add(new Edge(from, weight));
}
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int z = Integer.parseInt(st.nextToken());
int P = Integer.parseInt(br.readLine());
int mids[] = new int[P];
mids = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
minDist1 = new long[N+1]; minDist2 = new long[N+1];
findShortest(x, minDist1);
findShortest(z, minDist2);
for (int m : mids) {
if (minDist1[m]!=INF && minDist2[m]!=INF)
answer = Math.min(answer, minDist1[m]+minDist2[m]);
}
System.out.println((answer==INF)? -1:answer);
}
private static void findShortest(int start, long[] minDist) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(start, 0));
Arrays.fill(minDist, INF);
minDist[start] = 0;
while (!pq.isEmpty()) {
Edge now = pq.poll();
if (minDist[now.to] < now.weight) continue;
for (Edge e: edges[now.to]) {
if (minDist[e.to] > minDist[now.to] + e.weight) {
minDist[e.to] = e.weight + minDist[now.to];
pq.add(new Edge(e.to, minDist[e.to]));
}
}
}
}
}
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).