[ Algorithm ] 완전탐색 Brute-Force
코딩 테스트를 준비하면서 보다 탄탄한 기초를 위해 공부한 알고리즘을 하나씩 정리해보고자 한다.
본 포스트는 완전탐색에 대해 정리한 내용이다.
완전탐색 Brute-Force / Exhaustive search
완전탐색은 영어로 Brute-Force / Exhaustive search 라고 하고, 말 그대로 모든 경우의 수를 시도하는 방법이다. 완전탐색은 다음과 같은 경우에 자주 쓰인다.
- 구현이 간단하고, 해가 존재하면 항상 찾음
- 🔥 입력 값의 범위가 작은 경우
모든 경우의 수를 돌기 때문에 그만큼 경우의 수가 많아지면 시간을 많이 소요한다는 단점이 있기 때문에 주의해야 한다. 이에 해당하는 알고리즘으로 BFS, DFS, 비트마스크에 대해 정리하였다.
완전탐색 : BFS
너비 우선 탐색 BFS, Breadth-First Search 이란 루트 노드에서 시작해 인접한 노드를 먼저 탐색하는 방법을 말한다. 뒤에서 DFS 할 때도 나오겠지만, 이 두 알고리즘은 특히 ✅ 어떤 노드를 방문했는지 기억해야 한다. 이 부분이 빠진다면 무한루프에 빠질 위험이 있다.
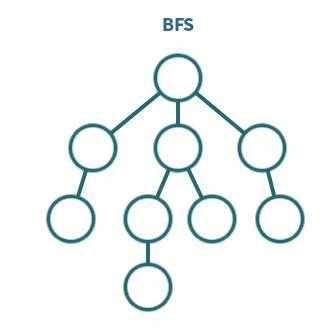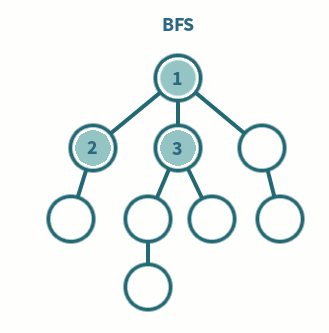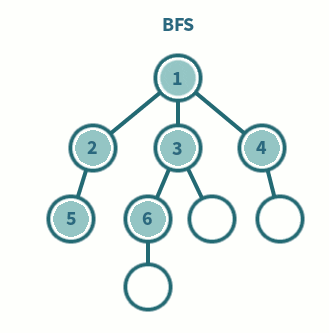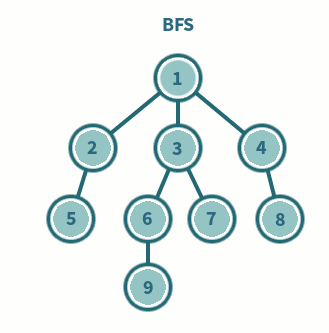
BFS 같은 경우는 방문한 노드를 차례로 in-out 할 수 있어야하기 때문에 FIFO First-In First-Out 큐를 사용한다. 해당 알고리즘은 두 노드 사이의 최단 경로를 찾거나 임의의 경로를 찾을 때 효과적으로 쓰인다.
간단한 예를 들어 이를 파이썬으로 구현해보자.
[문제]
X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력해라. 이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.
import sys
from collections import deque
def bfs(graph, start, route):
queue = deque(start)
while queue:
now = queue.popleft()
for node in graph[now]:
# if not visited
if route[node] == -1:
route[node] + route[now] + 1
queue.append(node)
return
city, road, distance, start = map(int, sys.stdin.readline().split())
route = [-1] * (city + 1)
route[start] = 0
graph = [[] for _ in range(city+1)]
# directed graph
for _ in range(road):
a, b = map(int, sys.stdin.readline().split())
graph[a].append(b)
bfs(graph, start, route)
# if answer distance K exist
if route.count(distance):
for i in range(1, city+1):
if route[i] == distance:
print(i)
else:
print(-1)
완전탐색 : DFS
깊이 우선 탐색 DFS, Depth-First Search 이란 루트 노드에서 시작해서 다음 브랜치로 넘어가기 전에 해당 브랜치를 끝까지 탐색하고 넘어가는 방법을 말한다.
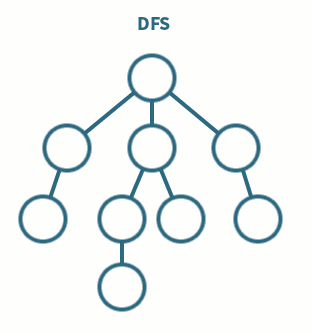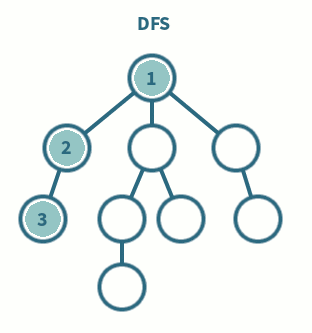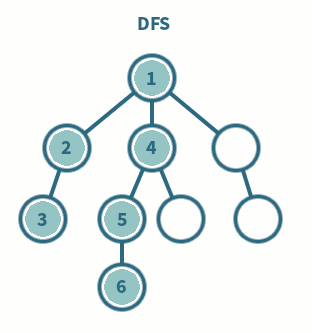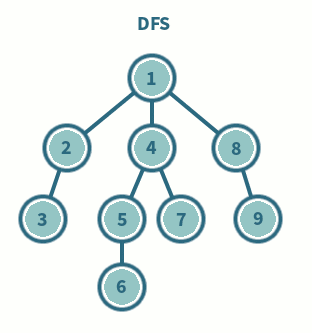
DFS는 재귀로 구현이 가능하며, BFS와 마찬가지로 ✅ 어떤 노드를 방문했는지 체크해줘야 한다. BFS보다 구현이 간단하다는 장점이 있지만, 단순 검색 속도는 상대적으로 느리다는 단점을 가지고 있다. DFS는 모든 노드를 방문할 때 주로 사용한다.
이번에도 간단한 예를 들어 파이썬으로 구현해보겠다.
[문제]
숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.
(1<= N <=9, 1<= number <=32000)
[예시] N = 5, number = 12
12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5
➡️ answer = 4
def solution (N, number):
answer = 0
# set : 중복 처리, in 탐색 유리
calc = [set() for i in range(9)]
# N < 8
for i in range(1, 9):
# possible number
# small << big
calc[i].add(int(str(N)*i))
for j in range(i//2 + 1):
# first, second for calculation (first < second)
for first in calc[j]:
for second in calc[i-j]:
calc[j].add(first + second)
calc[j].add(first - second)
calc[j].add(second - first)
calc[j].add(first * second)
if first != 0:
calc[j].add(second / first)
if second != 0:
calc[j].add(first / second)
# find the minimum Ns
if number in calc[j]:
return i
# 최솟값 > 8 : -1 반환
return -1
완전탐색 : 비트마스크
Q. 왜 비트마스크를 사용할까?
- DP, 순열, 배열 활용만으로 해결할 수 없는 문제를 해결하기 위해
- 적은 메모리 사용량
- 빠른 수행시간
- 집합을 배열의 인덱스로 표현할 수 있음
설명만으로는 감이 잘 오지 않으니, 아래 문제를 비트마스크로 접근해보자.
[문제]
비어있는 공집합 S가 주어졌을 때, 아래 연산을 수행하는 프로그램을 작성하시오.
(1 ≤ x ≤ 20)
* add x: S에 x를 추가한다. S에 x가 이미 있는 경우에는 연산을 무시한다.
* remove x: S에서 x를 제거한다. S에 x가 없는 경우에는 연산을 무시한다.
* check x: S에 x가 있으면 1을, 없으면 0을 출력한다.
* toggle x: S에 x가 있으면 x를 제거하고, 없으면 x를 추가한다.
* all: S를 {1, 2, ..., 20} 으로 바꾼다.
* empty: S를 공집합으로 바꾼다.
import sys
m = int(sys.stdin.readline())
s = 0b0
for _ in range(m):
order = sys.stdin.readline()
try:
command, num = order.split()
num = int(num)
if com == 'add':
s = s | (0b1 << num)
elif com == 'remove':
s = s & ~(0b1 << num)
elif com == 'check':
Related Posts
| Summary | 자료구조 Data Structure 정리 | |
| Summary | 디자인 패턴 & 프로그래밍 패러다임 | Design Pattern & Programming Paradigm | |
| Summary | 컴퓨터 구조 & 자료구조 | Computer Architecture & Data Structure |
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).