[ CS ] 컴퓨터 구조 & 자료구조 개념 Summary
CS 개념을 공부하고 다음에 볼 수 있도록 한 페이지에 정리해나가고자 한다. 참고한 페이지들은 밑에 첨부하였다. 가장 많이 도움이 되었던 건 gyoogle님의 신입 개발자 전공지식 & 기술 면접 백과사전! 더 자세한 내용을 공부하고 싶다면 아래 참고한 페이지를 보자!
Computer Architecture
캐시 메모리 Cache Memory
캐시 메모리는 쉽게 말하자면 속도가 빠른 장치와 느린 장치에서 속도 차이에 따른 병목 현상을 줄이기 위한 메모리이다.
CPU가 주기억장치에서 저장된 데이터를 읽어올 때, 자주 사용하는 데이터를 캐시 메모리에 저장하고, 다음에 이용할 때 주기억장치가 아닌 캐시 메모리에서 먼저 가져옴으로써 속도를 향상시키는 원리이다. 속도라는 장점은 있지만, 용량이 적고 비용이 높다는 단점이 있다.
- L1 : CPU 내부에 존재
- L2 : CPU와 RAM 사이에 존재
- L3 : 보통 메인보드에 존재
Data Structure
Array - LinkedList - ArrayList
비슷하게 느껴지는 위의 자료구조들을 정리하자.
Array: index로 빠르게 값을 찾을 수 있음LinkedList: 데이터의 삽입 및 삭제가 빠름ArrayList: (Java) 데이터를 빠르게 찾을 수 있지만, 삽입 및 삭제가 느림- 크기가 가변적인 배열이라고 생각하는 것이 직관적
- 데이터를 끝에 추가하는 연산에 많이 사용
연결리스트는 index를 가지고 있는 게 아니라 검색은 느리지만, 연결된 node의 포인터 위치 정보를 가지고 있기 때문에 중간에 삽입 및 삭제가 일어날 때 전체를 돌지 않아도 이전 값과 다음값이 가르켰던 주소값만 수정하여 연결시켜주면 되기 때문에 빠르게 진행할 수 있다. 또한, array는 메모리 상에 데이터가 연속적으로 저장되지만 리스트는 메모리 상에 데이터가 비연속적으로 저장된다는 특징을 가지고 있다.
스택 - 큐
📌 스택 Stack
한 쪽 방향으로 입출력이 제한되어 있는 자료 구조로, LIFO (Last in First Out, 후입선출) 구조를 따른다. 즉, 가장 나중에 들어온 것이 가장 먼저 나간다. 다음과 같은 경우에 활용할 수 있다.
- 웹 브라우저 방문기록 (뒤로 가기)
- 실행 취소
- 역순 문자열 만들기
- 후위 표기법 계산
- 하노이탑
📌 큐 Queue
입출력이 각각 다른 방향으로만 이루어지는 자료 구조로, FIFO (First in First Out, 선입선출) 구조를 따른다. 즉, 가장 먼저 들어온 것이 가장 먼저 나온다. 다음과 같은 경우에 활용할 수 있다.
- 은행 업무
- 우선순위 작업 예약
- 프로세스 관리
힙 Heap
힙은 우선순위 큐를 위해 만들어진 자료구조이다.
여기서, 우선순위 큐란 큐에 우선순위의 개념을 도입한 자료구조를 말한다. 스택과 큐도 우선순위 큐라고 할 수 있겠다. 우선순위 큐는 배열, 연결리스트, 힙으로 구현할 수 있는데 힙으로 구현하는 것이 가장 효율적이라고 한다.
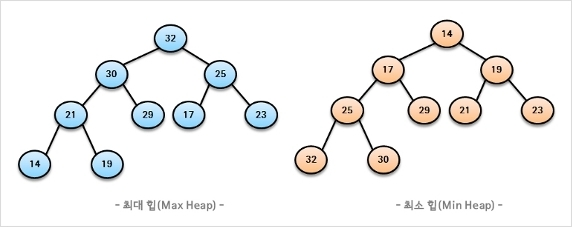
힙은 완전 이진 트리의 일종이며, 중복된 값이 허용된다는 점에서 이진 탐색 트리와 다르다. 완전 이진 트리는 여러 값 중 최댓값과 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다. 힙은 최대 힙과 최소 힙으로 나눠질 수 있으며, 최대 힙은 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리, 최소 힙은 반대라고 생각하면 된다. 구조는 다음과 같다.
힙을 저장하는 표준적인 자료구조는 배열로, 첫 번째 인덱스 0을 사용하지 않는다는 가정 하에 부모 노드와 자식 노드의 관계를 나타내면 아래와 같다.
left child index = (parent index) x 2
right child index = (parent index) x 2 + 1
parent index = (child index) // 2
- 📍 힙 삽입
- 새로운 노드를 힙의 마지막 노드에 삽입
- 새로운 노드를 부모 노드들과 교환
- 📍 힙 삭제
- 최대 힙에서 삭제는 최댓값 요소를 삭제
- 최대 힙에서 최댓값은 루트 노드! -> 삭제
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져와서 힙을 재구성
Reference
Related Posts
| Summary | 자료구조 Data Structure 정리 | |
| Summary | 디자인 패턴 & 프로그래밍 패러다임 | Design Pattern & Programming Paradigm | |
| Summary | Brute-Force Algorithm |
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).