[ AI / ML ] 머신러닝 - PCA (Principal Component Analysis)

👩🏻‍💻 K-MOOC 실습으로 배우는 머신러닝 강의

📙 해당 포스트는 K-MOOC 강의 내용과 추가로 다른 자료들을 찾아 내용을 작성하였으며, 이론 및 개념에 대해 공부하고 예제 실습도 진행한 후 내용을 정리하였다.

[ AI ] 인공지능과 머신러닝, 그리고 딥러닝와 같은 날 작성된 포스트이다.

목차

• [ AI / ML ] 머신러닝 - PCA (Principal Component Analysis) - 👩🏻‍💻 K-MOOC 실습으로 배우는 머신러닝 강의
  • 목차
  • 1. 주성분 분석 Principal Component Analysis
    • 따라서 PCA는 주로
  • 2. PCA의 원리 How It Works
  • 3. 분산을 최대로 보존할 수 있는 축을 선택하는 이유?
  • 4. PCA 적용
    • Step 1 : 데이터 정규화 (각 변수 값들의 평균 = 0)
    • Step 2 : 최적화 문제 정의
    • Step 3 : 최적해 도출
    • Step 4 : 고유벡터 (eigenvector) 들을 고유값 (eigenvalue) 기준으로 내림차순 정렬
    • Step 5 : 변수 추출을 통한 데이터 변환
    • Step 6 : 추출된 변수 중 일부만을 사용하여 데이터 역변환
  • 5. 결과 확인
  • 💻 실습 예제 코드
  • 마무리하면서..
    • 다음 포스트에서 만나요 🙌
  • 참고

1. 주성분 분석 Principal Component Analysis

차원축소(dimensionality reduction)와 변수추출(feature extraction) 기법으로 널리 쓰이고 있는 PCA (Principal Component Analysis)은 비지도학습 Unsupervised Learning에서 자료에 중복된 정보가 많을 경우, 자료가 갖는 차원보다 더 작은 수의 차원으로도 자료에 내재한 정보를 설명할 수 있을 것이라는 아이디어에서 소개된 개념이다.

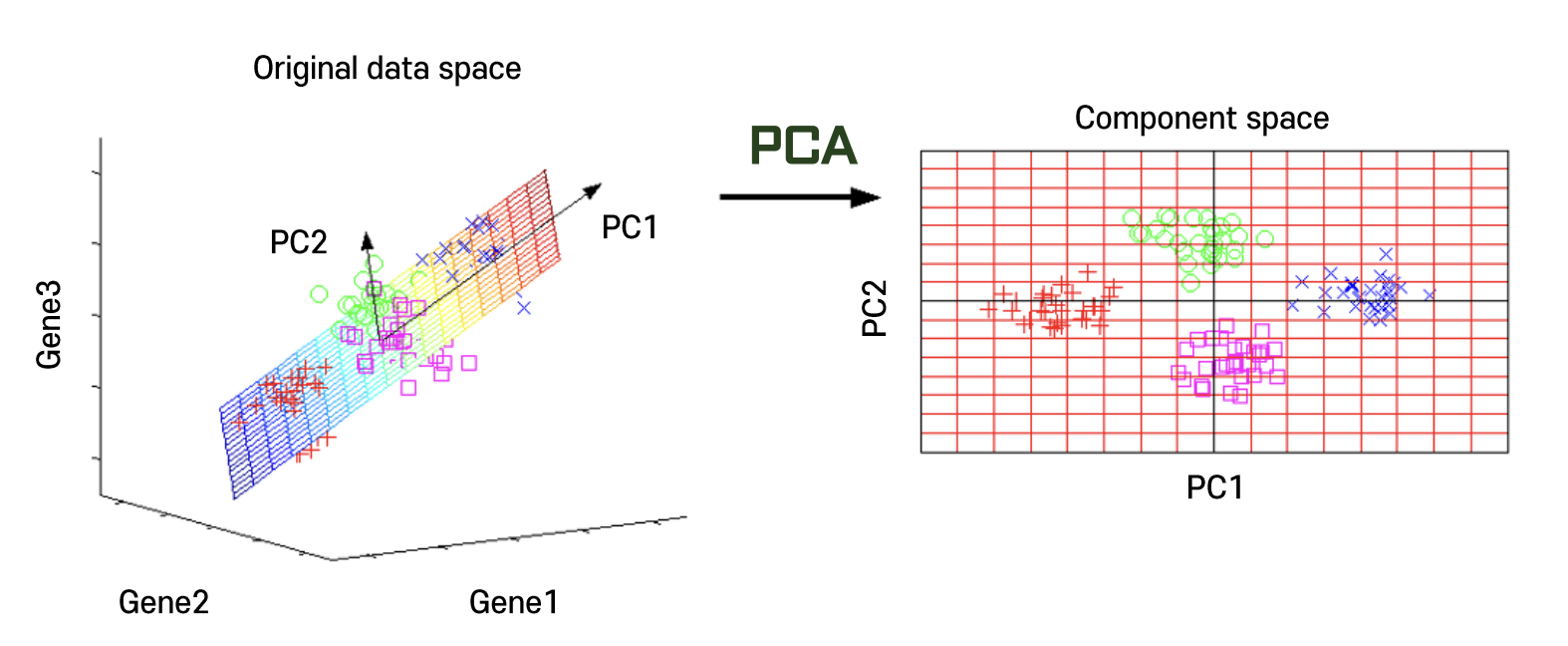
• 주성분이란
  • 전체 데이터 (독립변수)의 분산을 가장 잘 설명하는 성분
• 변수의 개수 = 차원의 개수
  → 차원이 증가할수록 데이터가 표현해야 하는 공간은 복잡해진다.
  

따라서 PCA는 주로

• 변수가 너무 많아 기존 변수를 조합해 새로운 변수를 가지고 모델링을 하려고 하거나
• 회귀 분석과 같은 종속관계 분석을 할 때 다중 공산성 multicollinearity을 없애기 위해 사용한다.

2. PCA의 원리 How It Works

데이터의 차원을 축소할 때 기존의 정보가 최대한 보존될 수 있는 새로운 축을 찾아야 한다. 이렇게 찾은 축을 Principle Component라고 하며, 주로 줄여서 PC라고 부른다.

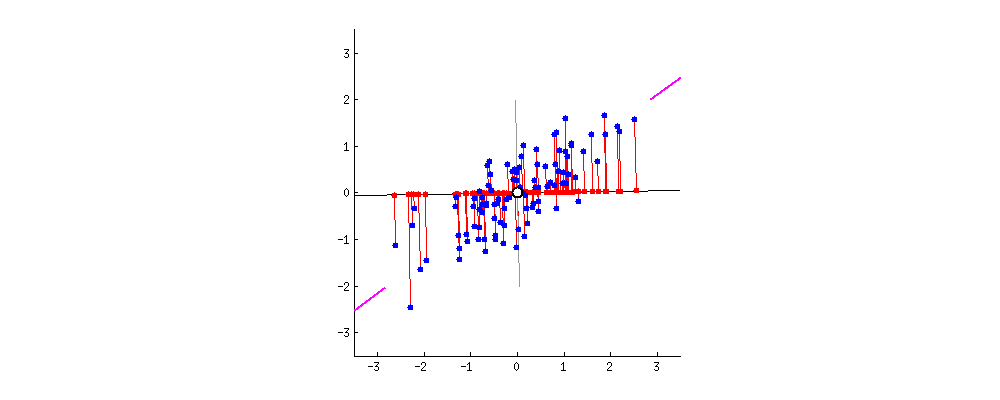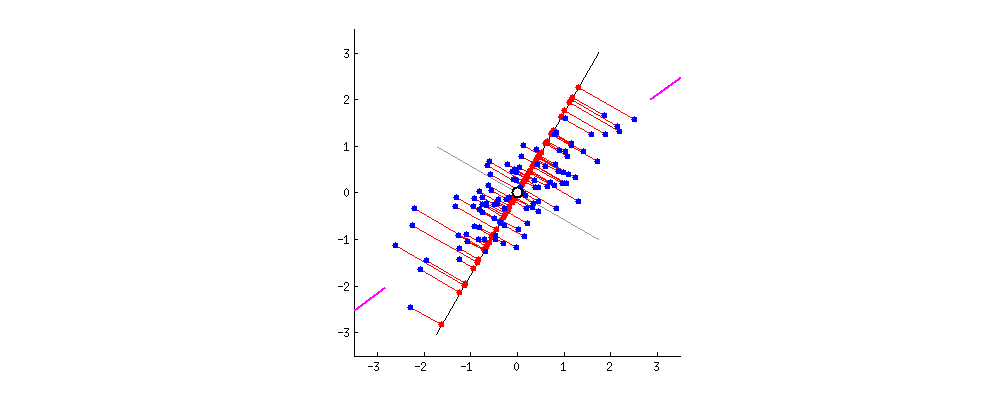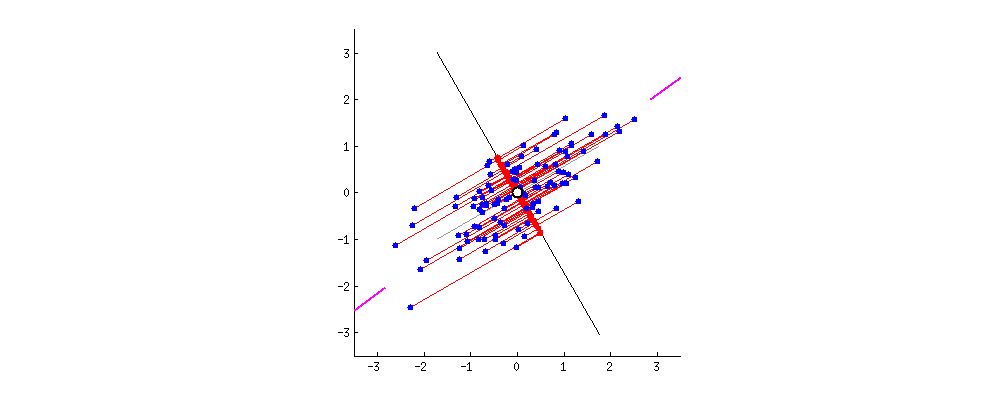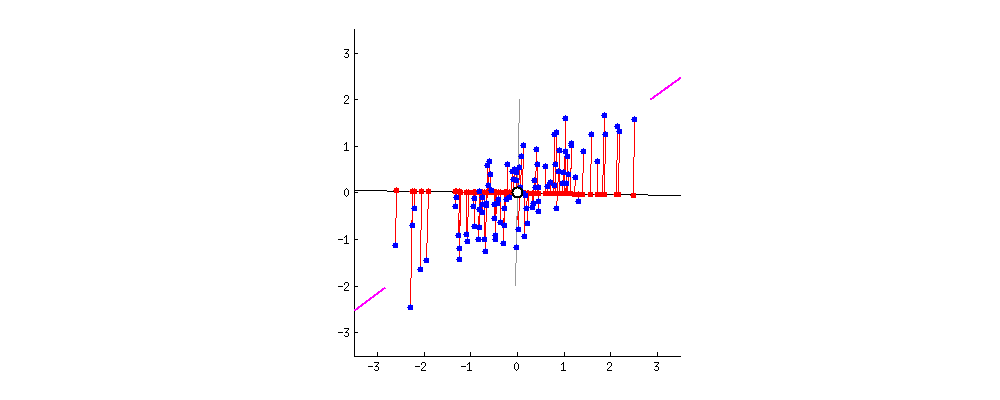
PC를 찾기 위해서는 covaiance matrix(공분산 행렬) 의 eigen vector(고유 벡터) 값을 찾아야 하고, 이 값 중 가장 큰 값이 우리가 원하는 PC 에 만족한다고 볼 수 있다.

3. 분산을 최대로 보존할 수 있는 축을 선택하는 이유?

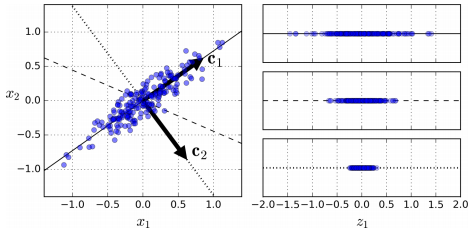
위의 그림처럼 간단한 2차원 데이터셋이 있을 때 c2의 직선을 선택하는 것이 분산을 가장 적게 나타내는 방법인데, 이렇게 되면 데이터를 유실하기가 쉬워진다.

따라서, 다른 방향으로 투영하는 것 보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있다. 분산이 커져야 데이터들사이의 차이점이 명확해지고, 그것이 모델을 더욱 좋은 방향으로 만들 수 있을 것이기 때문이다.

4. PCA 적용

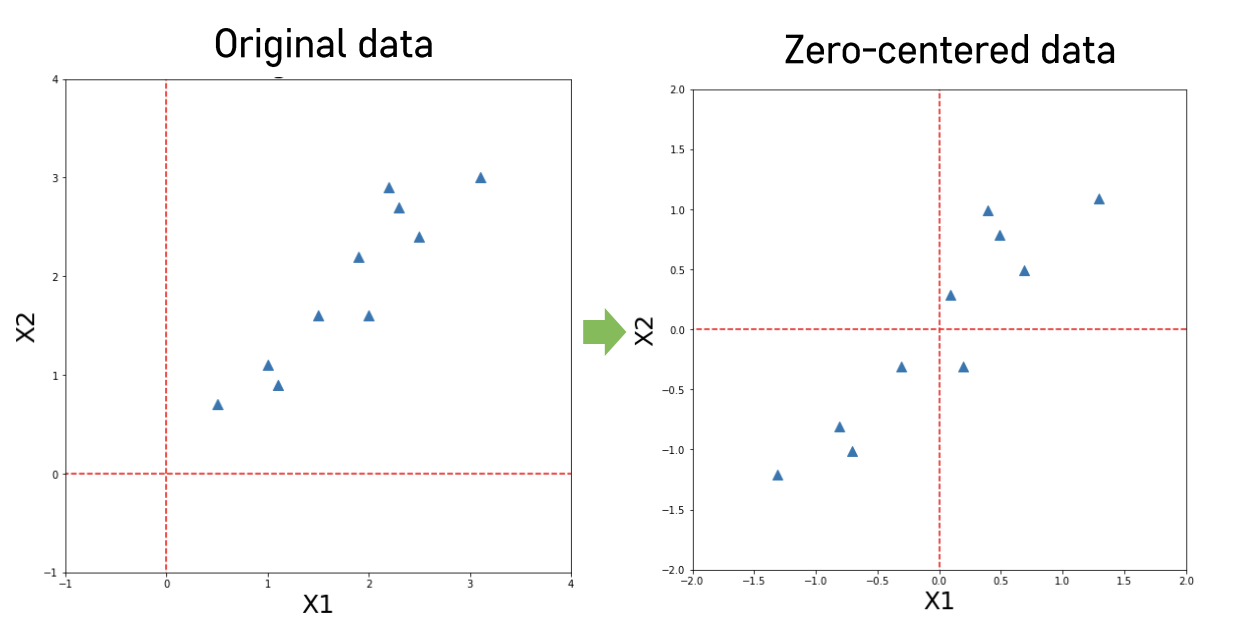
Step 1 : 데이터 정규화 (각 변수 값들의 평균 = 0)

Step 2 : 최적화 문제 정의

• 데이터를 사영시킨 후의 분산을 최대화하는 새로운 축을 찾는 것이 목표!

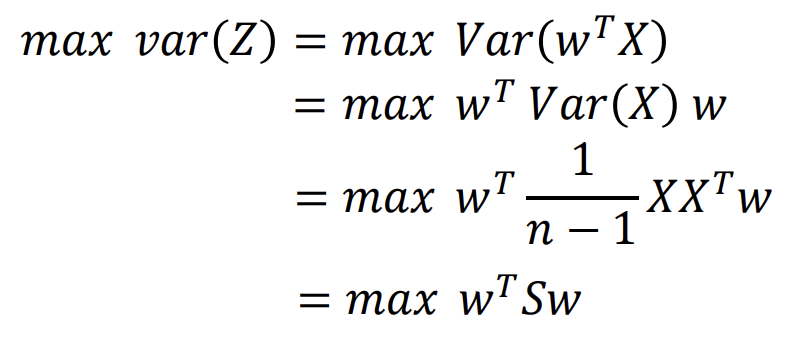
Step 3 : 최적해 도출

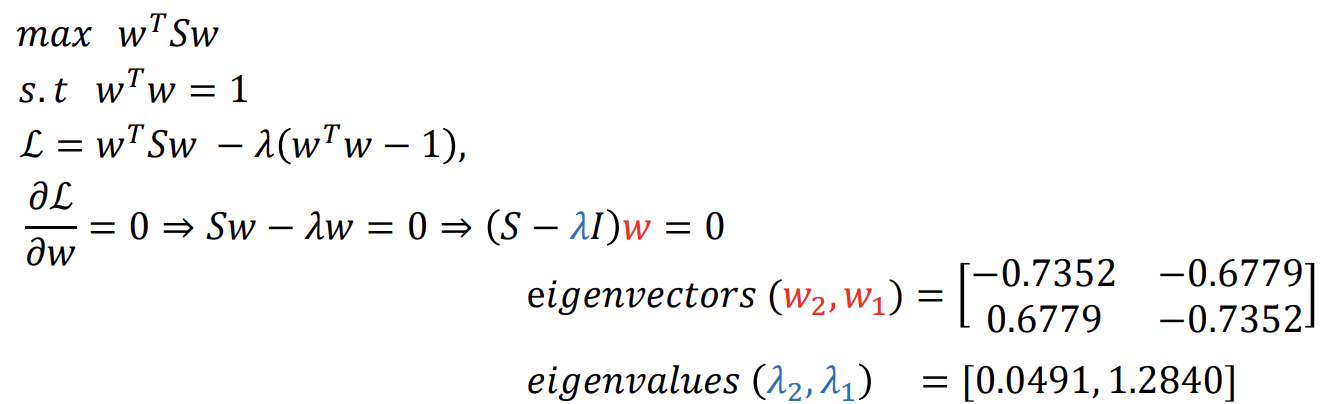
• Lagrangian multiplier를 사용하여 제약식을 목적식에 추가한 새 목적식 생성
• 새 목적식을 미분하여 기울기가 0이 되는 점에서 최적해 발생

Step 4 : 고유벡터 (eigenvector) 들을 고유값 (eigenvalue) 기준으로 내림차순 정렬

• 각 고유벡터는 선형변환된 공간에서 서로 직교하는 새로운 축이 됨

Step 5 : 변수 추출을 통한 데이터 변환

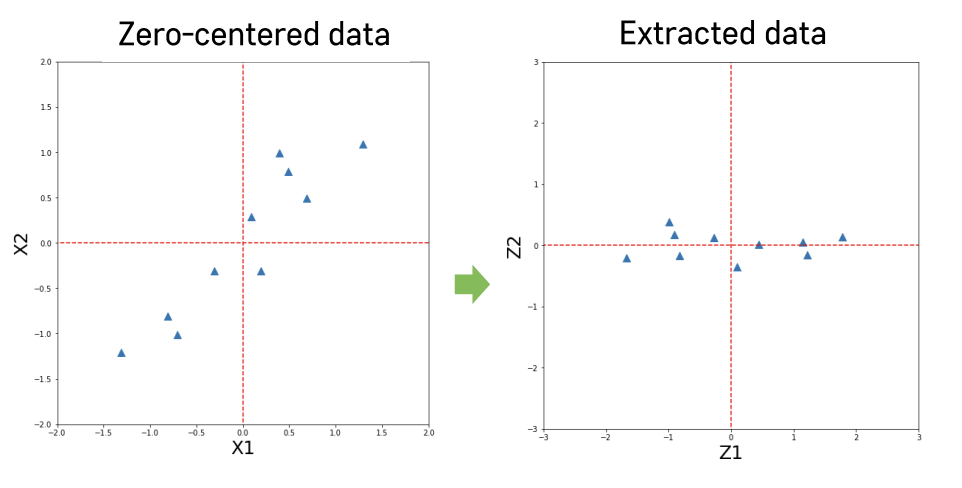
Step 6 : 추출된 변수 중 일부만을 사용하여 데이터 역변환

5. 결과 확인

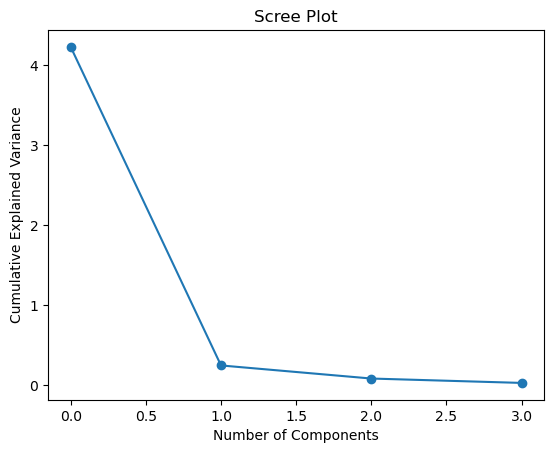
➡️ Scree Plot

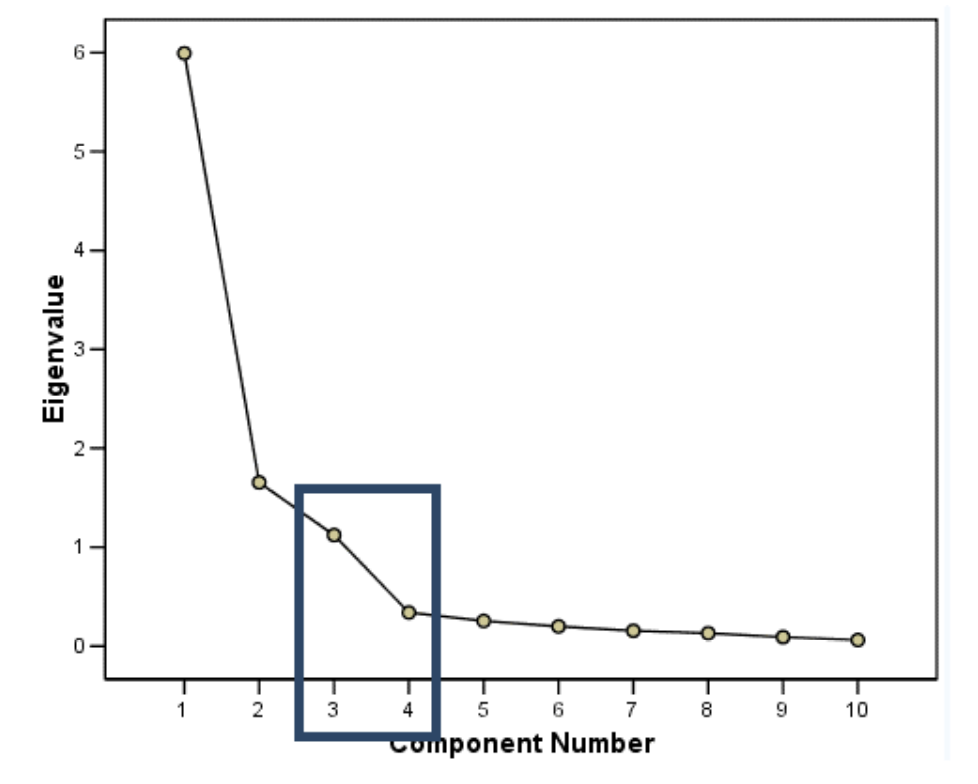
위의 그래프에서 네모친 곳처럼 정보의 감소량이 확 줄어드는 구간을 Elbow point라고 부른다. Eigenvalue의 Elbowpoint를 확인하고 적절하게 몇 차원으로 축소할지 결정한다.

➡️ Loading Plot

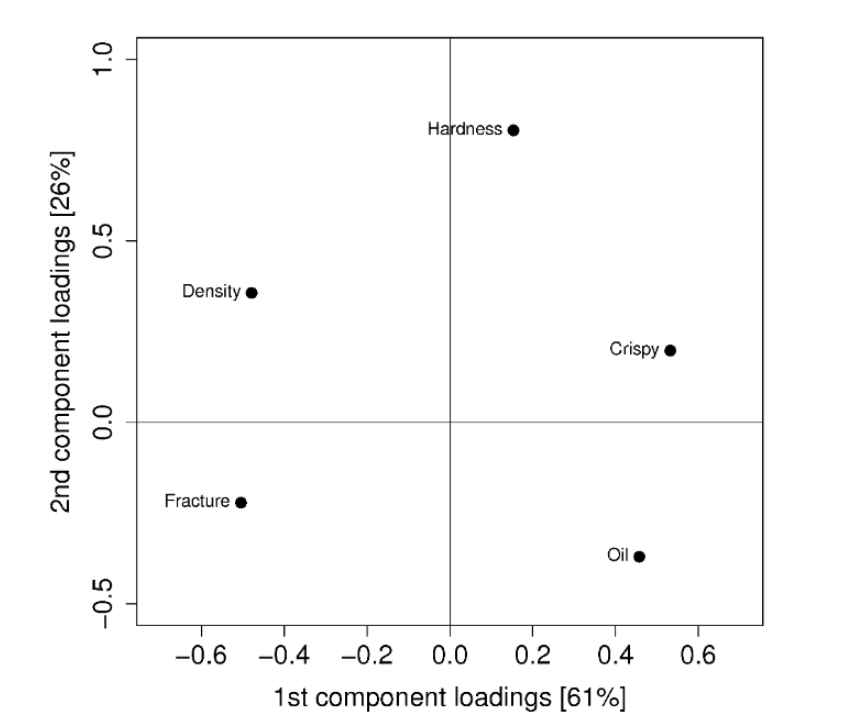
해당 plot은 각 주성분을 만들 때, 기존 데이터 x의 각 변수가 기여하는 정도를 판단하여 사후적인 변수에 대한 해석을 할 때 사용할 수 있다.

💻 실습 예제 코드

import seaborn as sns
import pandas as pd
from sklearn.decomposition import PCA

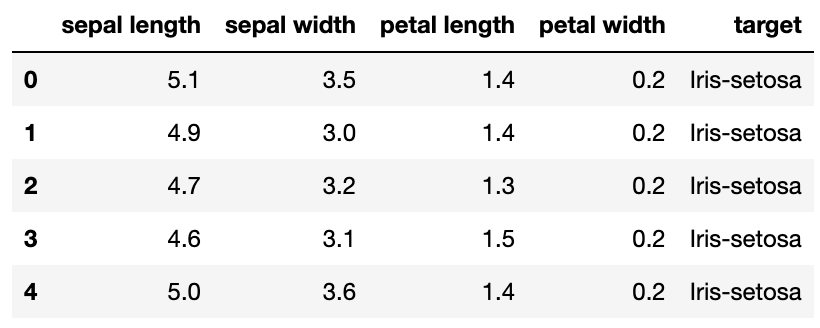
url = "https://archive.ics.uci.edu/ml/machine-learning-datebase/iris/irs.data"
df = pd.read_csv(url, 
                 naems = ['sepal length', 'sepal width', 'petal length',
                          'petal width', 'target'])

# Use only continuous data
data = df[df.columns[0:4]]

# Create PCA object with number of principal component
pca = PCA(n_components = len(df.columns) - 1)
pca_fit = pca.fit(data)

print('\n====== PCA Reulst Summary ======\n')
print('Singular value : \n', pca.singular_values_)
print('\n Singular vector : \n', pca.components_.T)
print('\n Explain Standard deviations : \n', np.sqrt(pca.explained_variance_))
print('\n Explain Variance Ratio : \n', pca.explained_variance_ratio_)
print('\n Noise Variance : \n', pca.noise_variance_)

====== PCA Reulst Summary ======

Singular value : 
 [25.08986398  6.00785254  3.42053538  1.87850234]

 Singular vector : 
 [[ 0.36158968  0.65653988 -0.58099728  0.31725455]
 [-0.08226889  0.72971237  0.59641809 -0.32409435]
 [ 0.85657211 -0.1757674   0.07252408 -0.47971899]
 [ 0.35884393 -0.07470647  0.54906091  0.75112056]]

 Explain Standard deviations : 
 [2.05544175 0.49218246 0.28022118 0.15389291]

 Explain Variance Ratio : 
 [0.92461621 0.05301557 0.01718514 0.00518309]

 Noise Variance : 
 0.0

# Scree Plot
plt.title("Scree Plot")
plt.xlabel("Number of Components")
plt.ylabel("Cumulative Explained Variance")
plt.plot(pca.explained_variance_, 'o-')

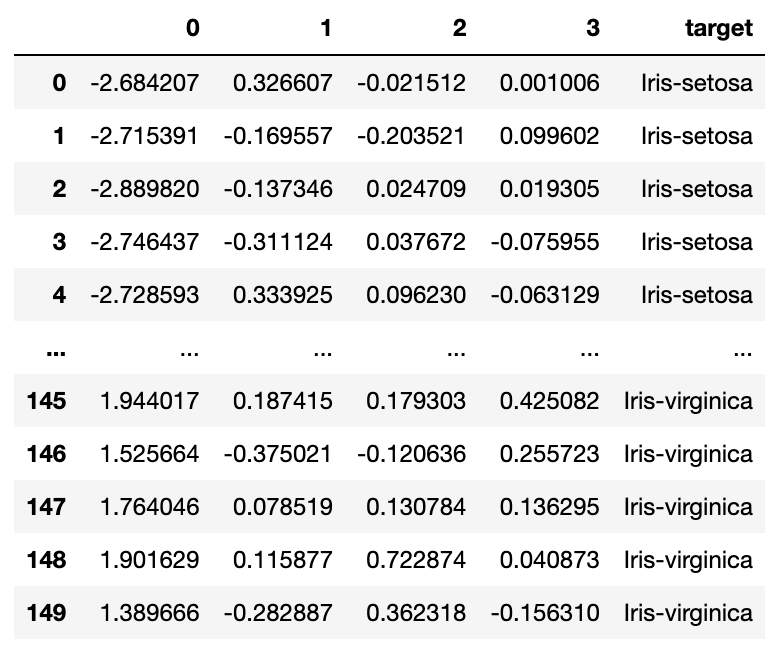
# get predict values
pca_pred = pd.DataFrame(pca.fit_transform(data))
pca_pred = pd.concat([pca_pred, df['target']], axis = 1)
pca_pred

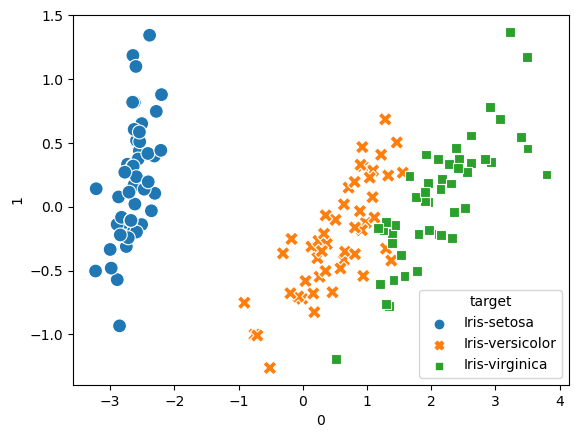
sns.scatterplot(pca_pred[0], pca_pred[1], data = pca_pred, hue = 'target',
                style = 'target', s = 100);

마무리하면서..

지도학습만 주로 다루다 보니 PCA는 개념만 알고 있고 직접 해볼 기회가 없었는데 이번에 해당 내용에 대해 정리하면서 우연히 차원 축소 실습 코드를 발견했다. 직접 해보니 간단하고 더 직관적으로 해당 내용에 대해 이해할 수 있었다. 비지도학습을 다루게 되는 그 어느 날 오늘 공부한 내용이 도움이 되길!!

다음 포스트에서 만나요 🙌

참고

K-MOOC 실습으로 배우는 머신러닝

머신러닝 - PCA (Principal Component Analysis)

Stack Exchange - Making sense of principal component analysis, eigenvectors & eigenvalues

[sklearn] PCA (Principal Component Analysis)