[ AI / ML ] 머신러닝 - 군집화 (Clustering)
👩🏻💻 K-MOOC 실습으로 배우는 머신러닝 강의
📙 해당 포스트는 K-MOOC 강의 내용과 추가로 다른 자료들을 찾아 내용을 작성하였으며, 이론 및 개념에 대해 공부하고 예제 실습도 진행한 후 내용을 정리하였다.
[ AI ] 인공지능과 머신러닝, 그리고 딥러닝와 같은 날 작성된 포스트이다.
1. 군집화 Clustering
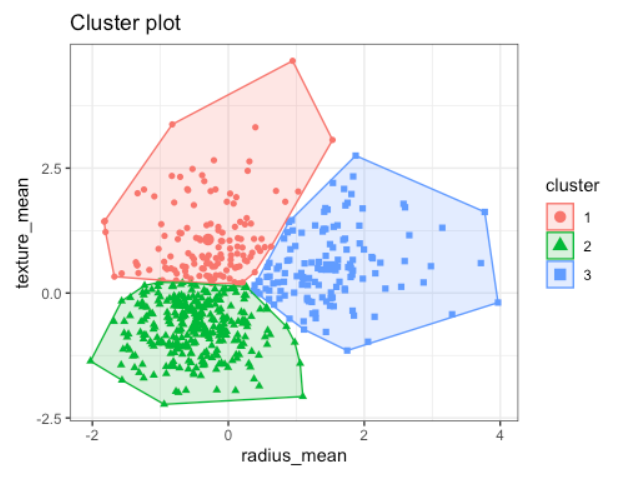
유사한 속성들을 갖는 관측치를 묶어 전체 데이터를 몇 개의 군집 (그룹) 으로 나누는 것을 군집화라 한다.
- 군집화 기준
- 군집 내 유사도 최대화
- 동일한 군집에 속한 관측치들은 서로 유사할수록 좋음
- 군집 간 유사도 최소화
- 상이한 군집에 속한 관측치들은 서로 다를수록 좋음
- 군집 내 유사도 최대화
2. 분류와 군집화는 어떻게 다를까?
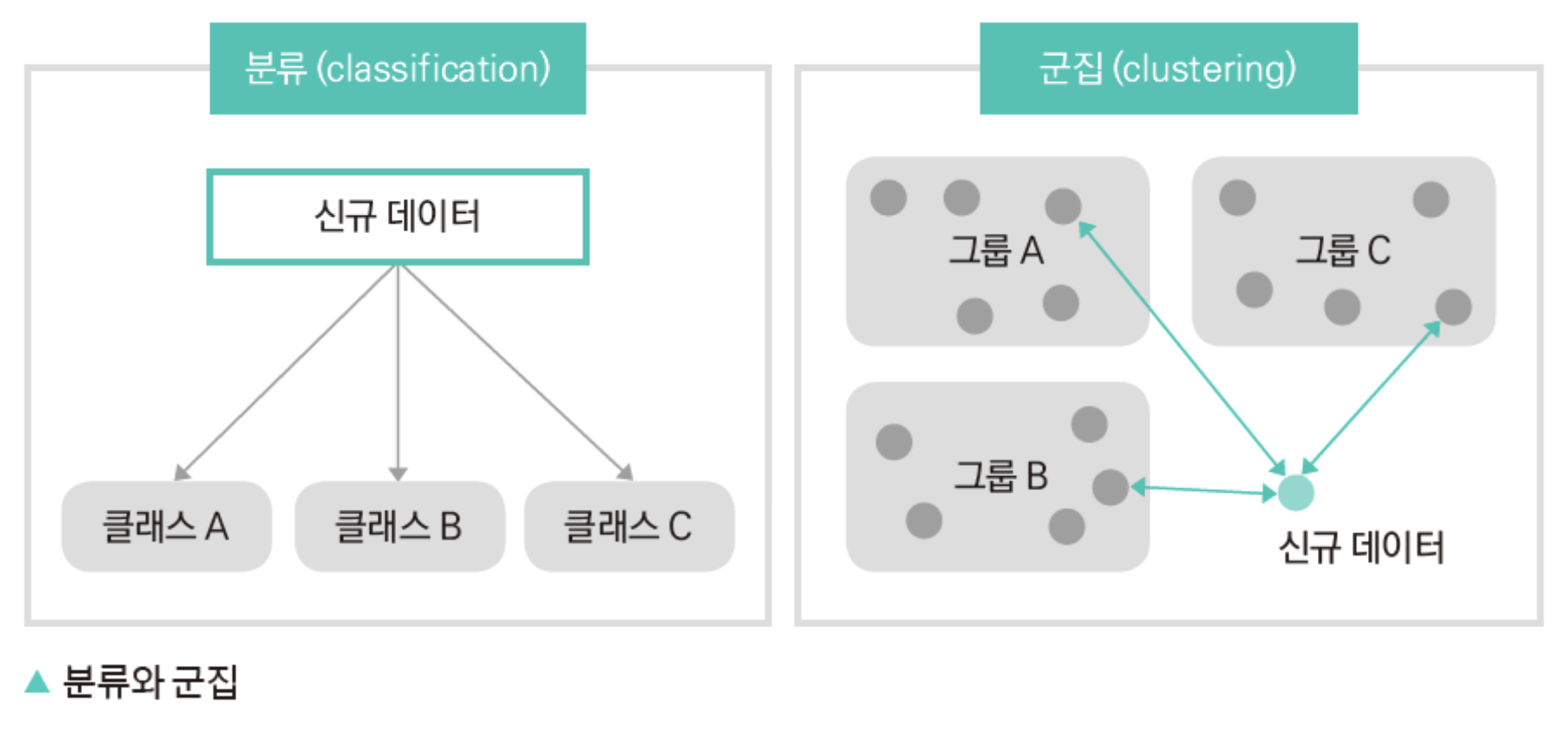
- 분류 Classification
- 사전 정의된 범주가 있는 labeled data로부터 예측 모델을 학습하는 문제
- Supervised Learning (지도 학습)
- 군집화 Clustering
- 사전 정의된 범주가 없는 unlabeled data에서 최적의 그룹을 찾아나가는 문제
- Unsupervised Learning (비지도 학습)
3. 군집화 활용 Application
군집화는 특히 세분화 Segmentation에서 활용된다.
- E-commerce
- 온라인 쇼핑몰
- 고객 특정 유형으로 분류 ➡️ 맞춤 서비스 제공
- 새로운 고객 유형 발견 ➡️ 마케팅 전략에 활용
- 온라인 쇼핑몰
-
유사 문서 군집화
-
서울시 오존 농도의 패턴 군집화 (25개 구)
- Tracking
- 이미지 / 영상
- Anomaly detection
- 이상검출
- 제조 / 물류 분야
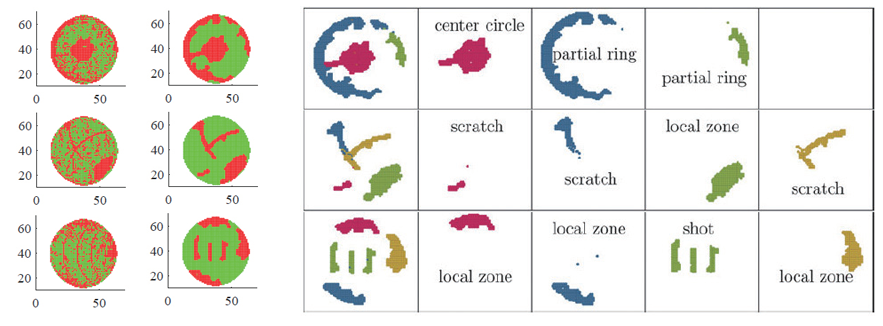
- 반도체 웨이퍼의 fail bit map 군집화
4. 군집화 알고리즘 Clustering Algorithm
- K-Means (Centroid)
- Hierarchical
- DBSCAN (밀도)
✔️ K-Means (Centroid)
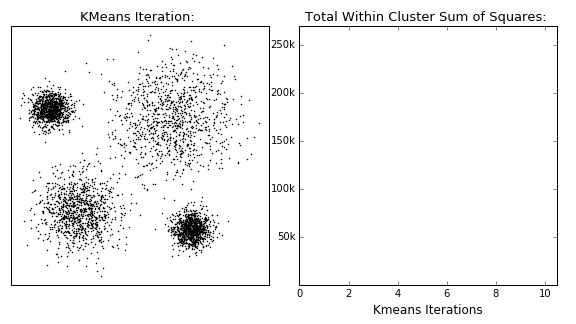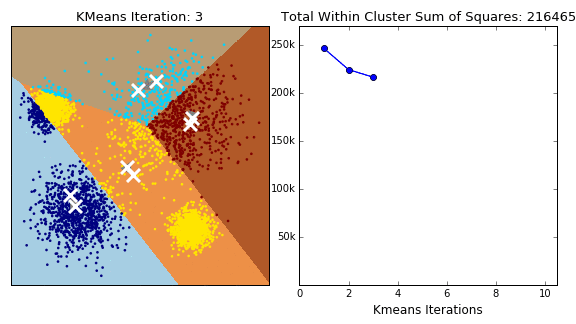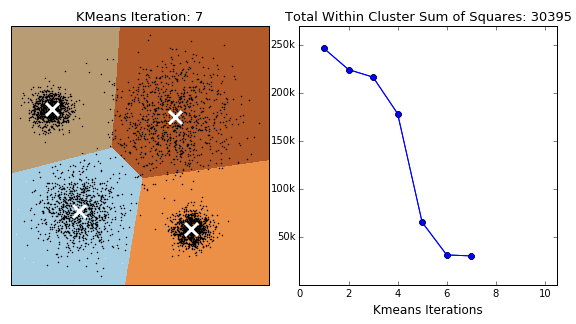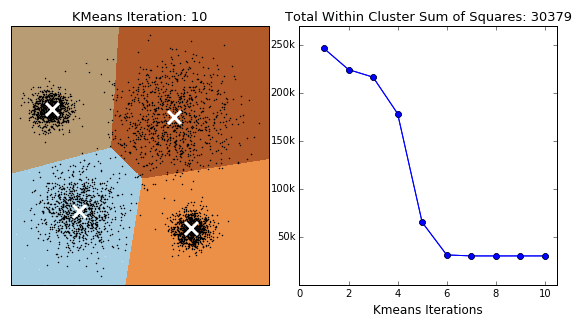
K-Means는 군집 중심점 Centroid 기반의 클러스터링 중 하나로, 일반적으로 가장 쉽고 많이 사용되는 알고리즘이다.
예를 들어, A,B,C,D,E,F 와 같이 5개의 데이터 세트가 주어지고 2개의 군집을 형성시키고 싶다.
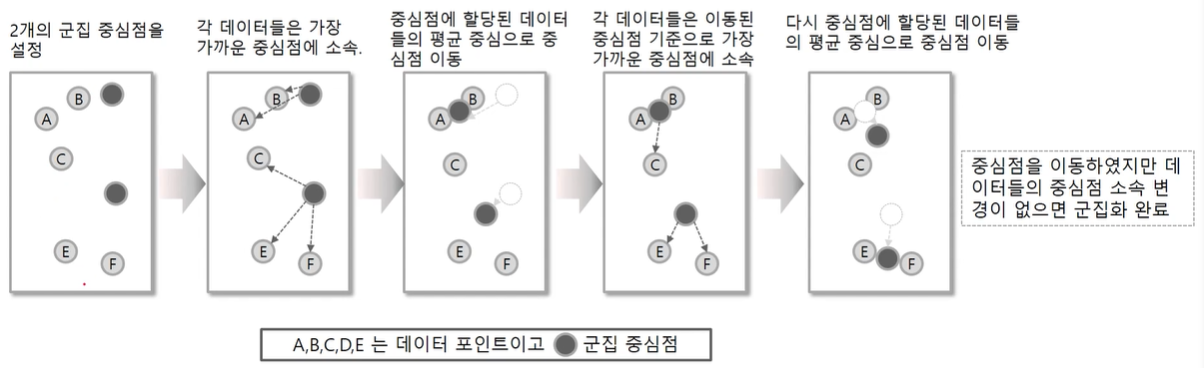
- 먼저 임의의 2개 검은점 Centroid를 만든다.
- 각 A,B,C,D,E 데이터는 2개의 Centroid와의 거리를 확인한 다음, 가까운 Centroid에 소속이 된다.
- 소속이 결정되면 각 데이터의 중심 공간으로 Centrod들이 이동한다.
- 다시 A,B,C,D,E 데이터들은 각 Centroid와 거리를 계산하여 가까운 Centroid에 소속이 된다.(3번째그림)
- C데이터는 전과 다르게 다른 Centroid에 소속이 된것을 확인할 수 있다.(4번째 그림)
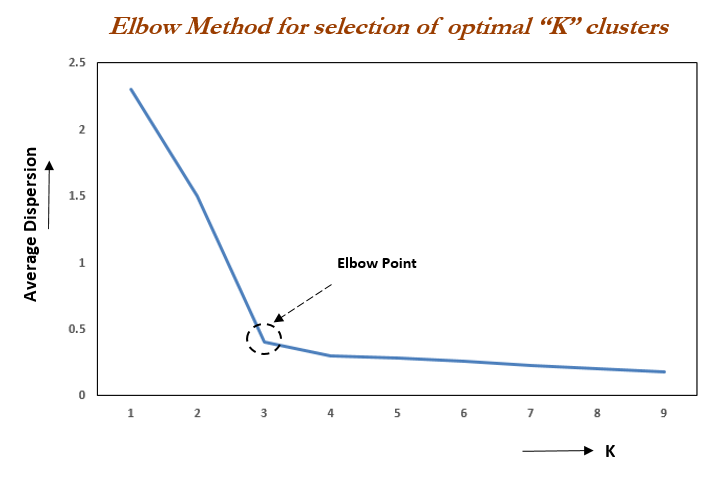
- 각 Centroid는 다시 자신의 속한 데이터들의 중심으로 이동하게 되고, 더이상 각 데이터들이 Centroid 소속이 변경되지 않는다면 종료된다. (Elbow point)
장점
- 일반적으로 가장 많이 활용되는 알고리즘으로, 가장 쉽고 간결하다.
- 대용량 데이터에서도 활용이 가능하다.
단점
- 거리기반 알고리즘으로 속성 개수가 많으면 군집화 정확도가 떨어지며, PCA로 차원 축소를 진행할 수 있다.
- 반복횟수가 많아질 경우 수행시간이 느려지고, 이상치 (outlier) 에 민감하다.
✔️ Hierarchical Clustering
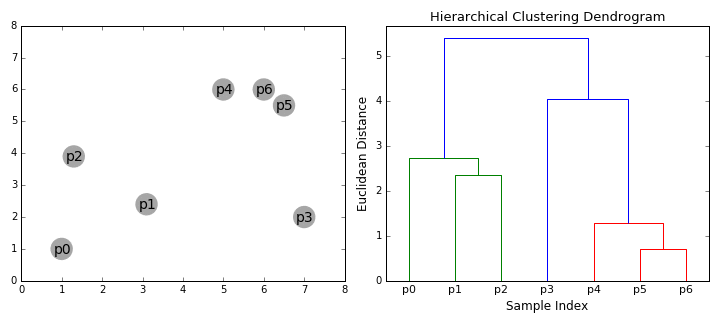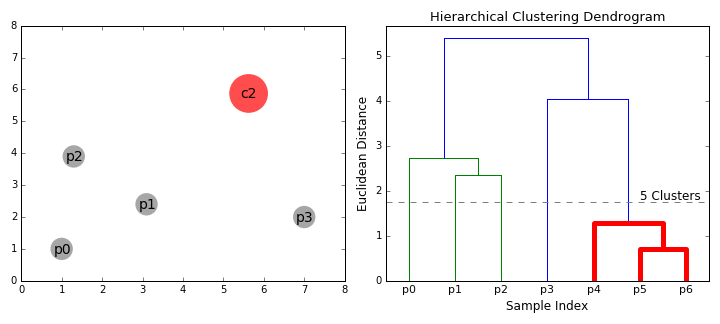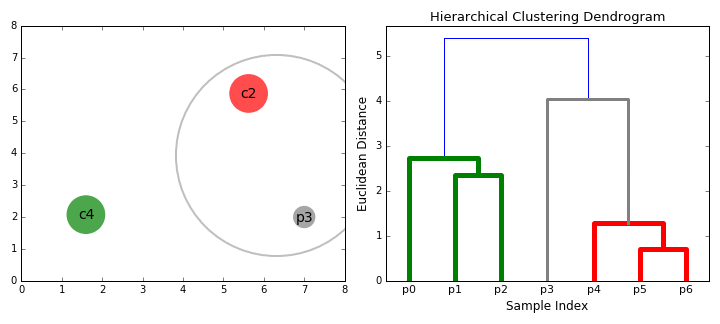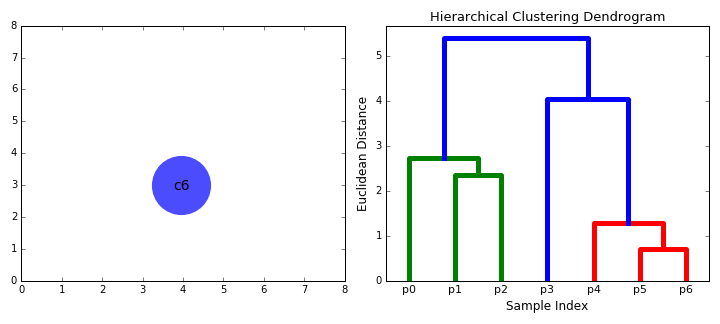
계층적 군집화 Hierarchical Clustering 는 여러개의 군집 중에서 가장 유사도가 높은 혹은 거리가 가까운 군집 두 개를 선택하여 하나로 합치면서 군집 개수를 줄여 가는 방법을 말한다. 다른 말로 합체 군집화(agglomerative clustering)이라고 불리기도 한다.
🤔 군집간의 거리 측정
계측정 군집화를 하려면 우선 모든 군집 간에 거리를 측정해야 한다. 군집 간의 거리를 측정하는 방법에는 계층적 방법에 의존하지 않는 비계층적 방법과 이미 이전 단계에서 계층적 방법으로 군집이 합쳐진 적인 있다는 가정을 하는 계층적 방법 두 가지가 있다.
1. 비계층적 거리 측정법
비계층적 거리 측정법은 계층적 군집화가 아니더라도 모든 경우에 사용할 수 있는 거리 측정 방법이다. 중심 / 단일 / 완전 / 평균 거리 등이 있고, 계층적 거리 측정법에 비해 계산량이 많은 단점이 있다.
2. 계층적 거리 측정법
계층적 거리 측정법은 계층적 군집화에서만 사용할 수 있는 방법이다. 즉, 이전 단계에서 이미 어떤 두 개의 군집이 하나로 합쳐진 적이 있다고 가정하여 이 정보를 사용하는 측정법이다. 비계층적 거리 측정법에 비해 계산량이 적어 효율적이다.
✔️ DBSCAN Density-Based Spatial Clustering of Applications with Noise
K-Means 군집화 방법은 단순하고 강력한 방법이지만 군집의 모양이 원형이 아닌 경우에는 잘 동작하지 않으며, 사용자가 군집의 개수를 지정해주어야 한다는 단점이 있다.
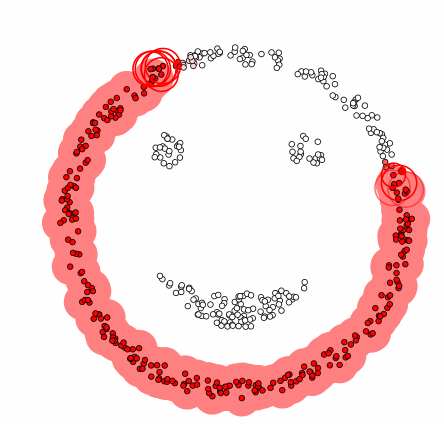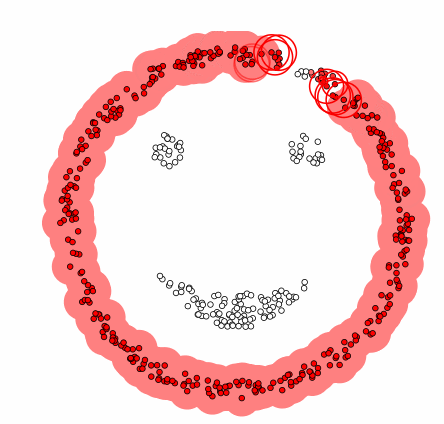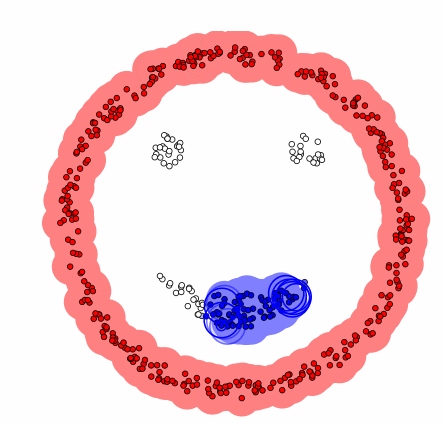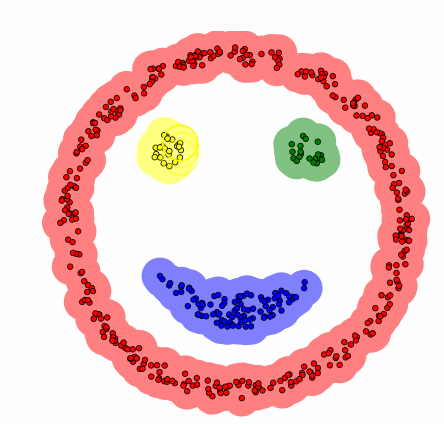
DBSCAN 군집화 방법은 데이터가 밀집한 정도 즉 밀도를 이용한다. DBSCAN 군집화는 군집의 형태에 구애받지 않으며 군집의 갯수를 사용자가 지정할 필요가 없다. 디비스캔 군집화 방법에서는 초기 데이터로부터 근접한 데이터를 찾아나가는 방법으로 군집을 확장한다.
5. 군집화 결과 측정 및 평가
- SSE Sum of Squared Error
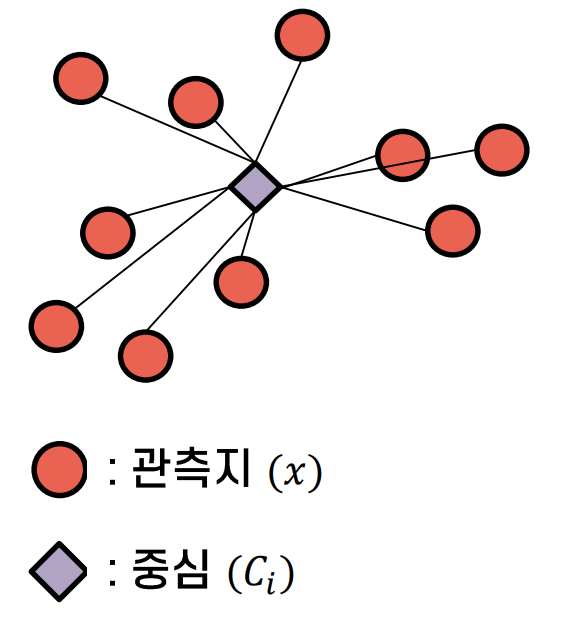
- 수식
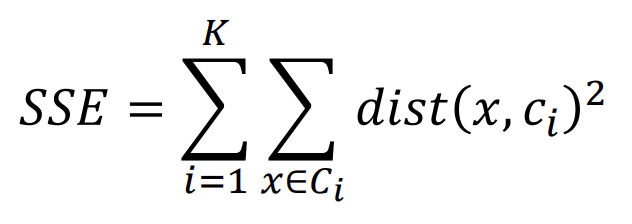
- 그래프
- 수식
-
Silhouette
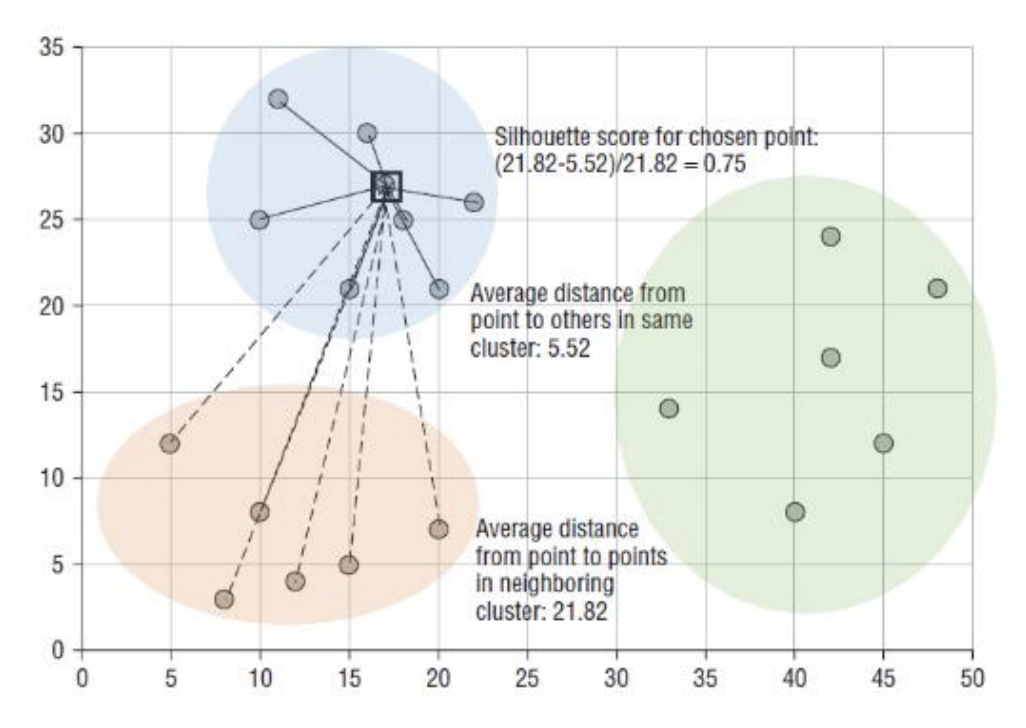
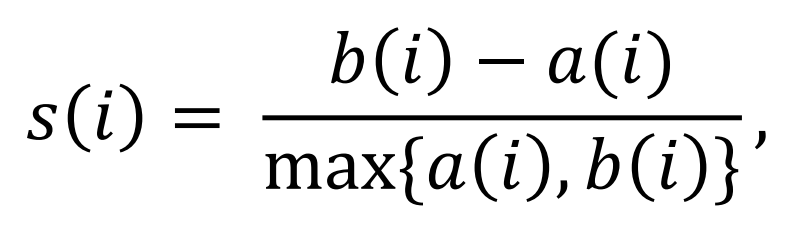
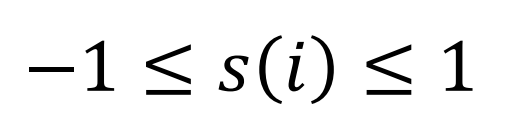 ➡️
➡️ 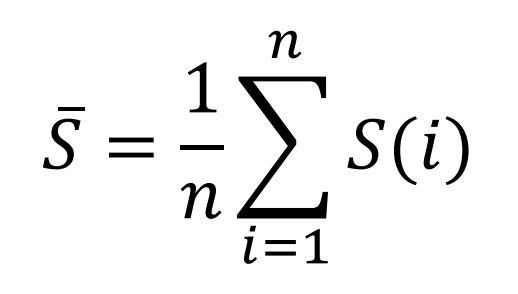
- a(i)
- 관측치 i로부터 같은 군집 내에 있는 모든 다른 개체들 사이의 평균 거리
- b(i)
- 관측치 i로부터 다른 군집 내에 있는 개체들 사이의 평균 거리 중 최솟값
- 일반적으로 0.5보다 크면 군집 결과가 타당하다고 볼 수 있음
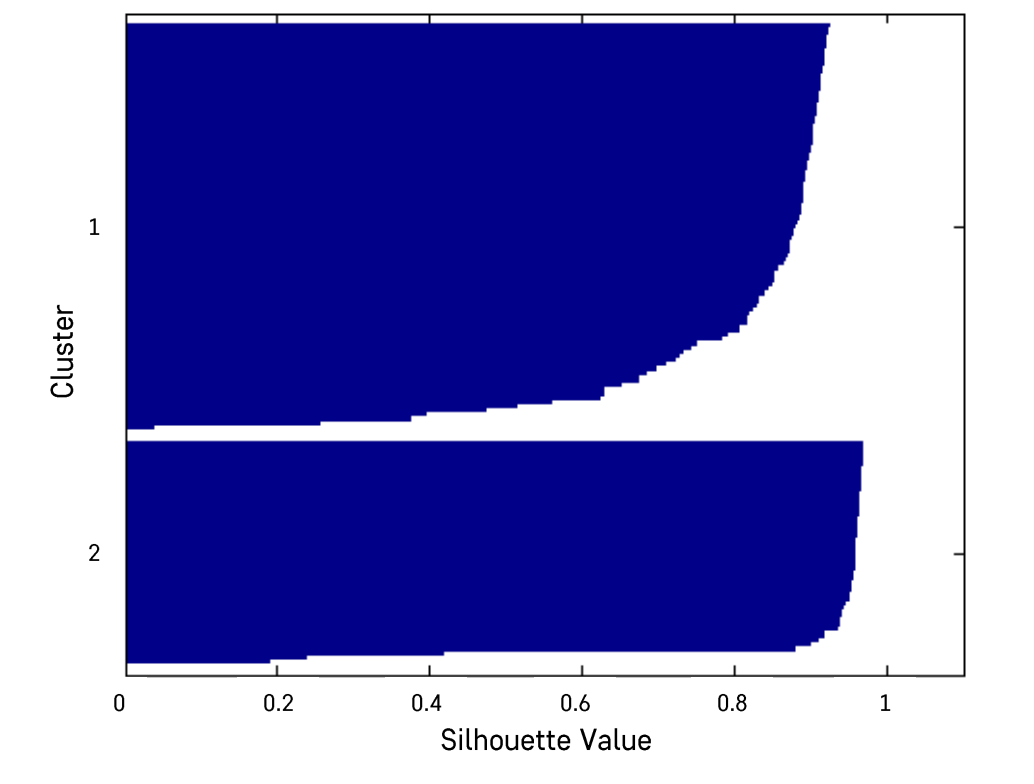
- a(i)
💻 실습 예제 코드
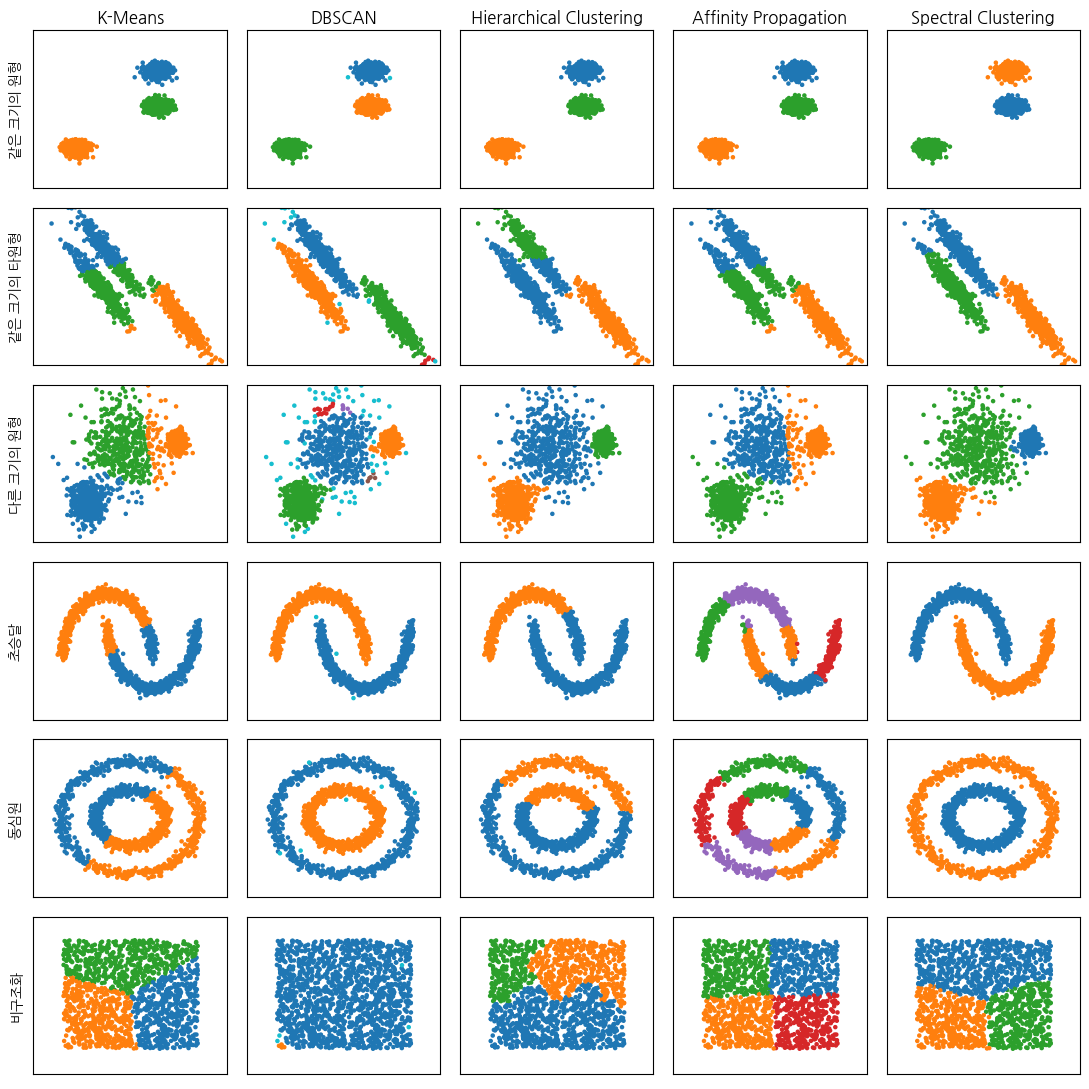
다음은 몇 가지 예제 데이터에 대해 위에서 나열한 군집화 방법을 적용한 결과이다. 같은 색상의 데이터는 같은 군집로 분류된 것이다. 그림에서도 볼 수 있지만 각 군집화 방법마다 특성이 다르므로 원하는 목적과 데이터 유형에 맞게 사용해야 한다.
from sklearn.datasets import *
from sklearn.cluster import *
from sklearn.preprocessing import StandardScaler
from sklearn.utils._testing import ignore_warnings
np.random.seed(0)
n_samples = 1500
blobs = make_blobs(n_samples=n_samples, random_state=8)
X, y = make_blobs(n_samples=n_samples, random_state=170)
anisotropic = (np.dot(X, [[0.6, -0.6], [-0.4, 0.8]]), y)
varied = make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=170)
noisy_circles = make_circles(n_samples=n_samples, factor=.5, noise=.05)
noisy_moons = make_moons(n_samples=n_samples, noise=.05)
no_structure = np.random.rand(n_samples, 2), None
datasets = {
"같은 크기의 원형": blobs,
"같은 크기의 타원형": anisotropic,
"다른 크기의 원형": varied,
"초승달": noisy_moons,
"동심원": noisy_circles,
"비구조화": no_structure
}
plt.figure(figsize=(11, 11))
plot_num = 1
for i, (data_name, (X, y)) in enumerate(datasets.items()):
if data_name in ["초승달", "동심원"]:
n_clusters = 2
else:
n_clusters = 3
X = StandardScaler().fit_transform(X)
two_means = MiniBatchKMeans(n_clusters=n_clusters)
dbscan = DBSCAN(eps=0.15)
spectral = SpectralClustering(n_clusters=n_clusters, affinity="nearest_neighbors")
ward = AgglomerativeClustering(n_clusters=n_clusters)
affinity_propagation = AffinityPropagation(damping=0.9, preference=-200)
clustering_algorithms = (
('K-Means', two_means),
('DBSCAN', dbscan),
('Hierarchical Clustering', ward),
('Affinity Propagation', affinity_propagation),
('Spectral Clustering', spectral),
)
for j, (name, algorithm) in enumerate(clustering_algorithms):
with ignore_warnings(category=UserWarning):
algorithm.fit(X)
if hasattr(algorithm, 'labels_'):
y_pred = algorithm.labels_.astype(np.int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i == 0:
plt.title(name)
if j == 0:
plt.ylabel(data_name)
colors = plt.cm.tab10(np.arange(20, dtype=int))
plt.scatter(X[:, 0], X[:, 1], s=5, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plot_num += 1
plt.tight_layout()
plt.show()
마무리하면서..
다음 포스트에서 만나요 🙌
다음 포스트에서는 해당 내용을 바탕으로 실습을 해볼 예정이다.
참고
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).