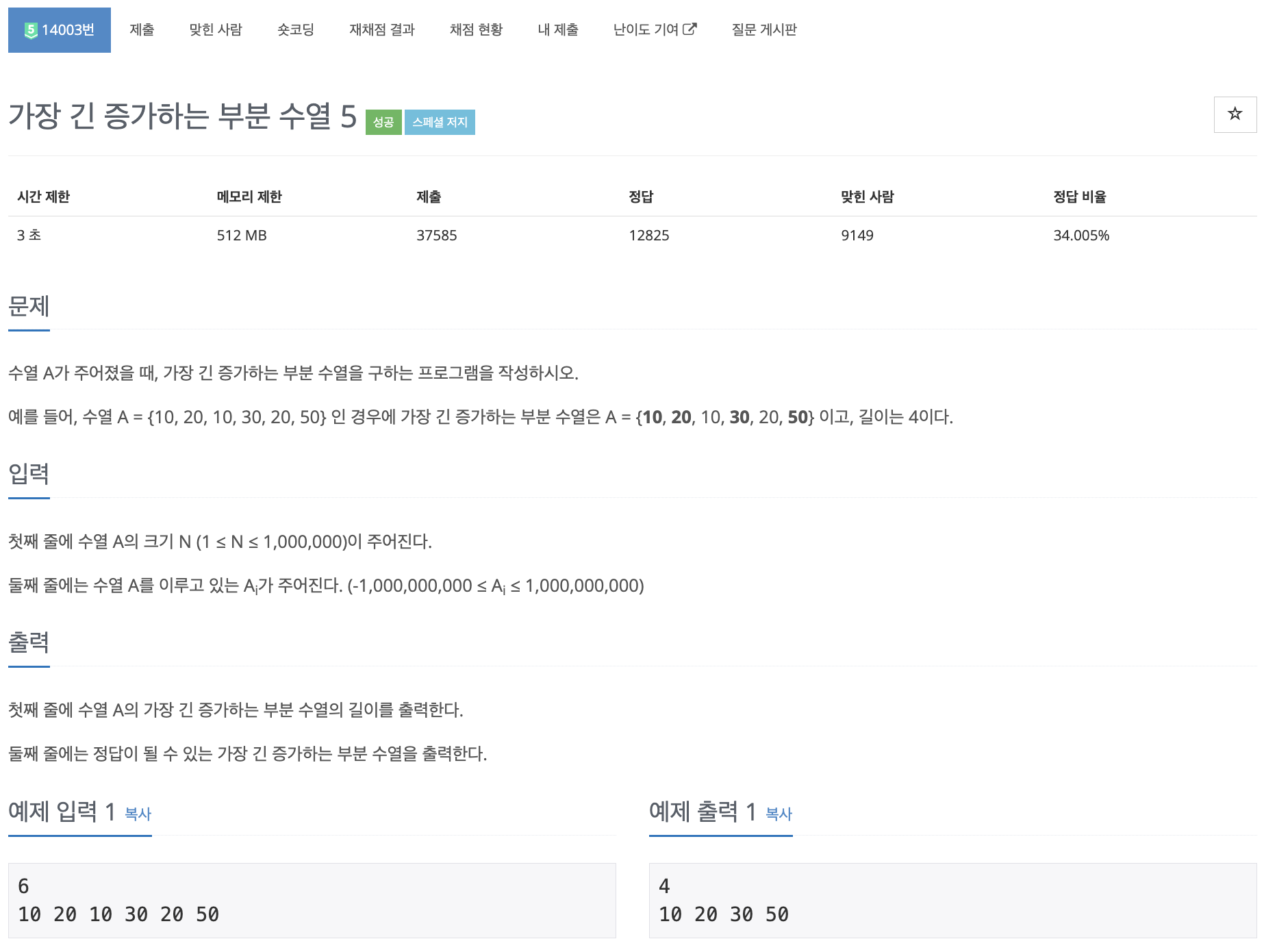
BOJ 백준 14003번 가장 긴 증가하는 부분 수열 5 | Java

🔎 문제 설명

🩵 플레 5

- 난이도 ★★☆☆
- LIS

LIS, Longest Increasing Subsequence

LIS 문제의 가장 흔한 풀이는 DP 동적프로그래밍이다. 그러나 이 문제 같은 경우는 N이 1백 만까지로 일반적인 DP 풀이 방법으로 하게 된다면 시간복잡도는 \(O(N^2) = 10^{12}\) 로 약 1만 초가 소요되므로 시간초과가 난다. 괜히 플레가 아님.. 나도 이분탐색으로 푸는 방법을 몰랐다면 지금도 울고 있었겠지 하하!

이분탐색으로 LIS 풀기

LIS 문제를 푸는 다른 방법으로는 이분 탐색이 있다! 쉽게 말하자면 크기를 고려해서 리스트에 넣다보니 결국 그게 LIS의 최종길이일 수 밖에 없다는 건데..!

먼저 리스트 list 를 준비하고 주어진 수열을 하나씩 돌면서 이분탐색을 이용해 list에 들어갈 인덱스 위치를 찾는다.

1. 만약 들어갈 위치가 list 사이즈보다 작다면 ▶️ 해당 위치의 값을 현재 값으로 갱신
2. list 사이즈랑 같다면 (LIS 배열의 최장길이가 갱신되는 경우) ▶️ list 마지막에 추가해준다.

아직도 이해가 안 된다면 아래 그림을 참고하면 무슨 말인지 대충 이해가 된다.

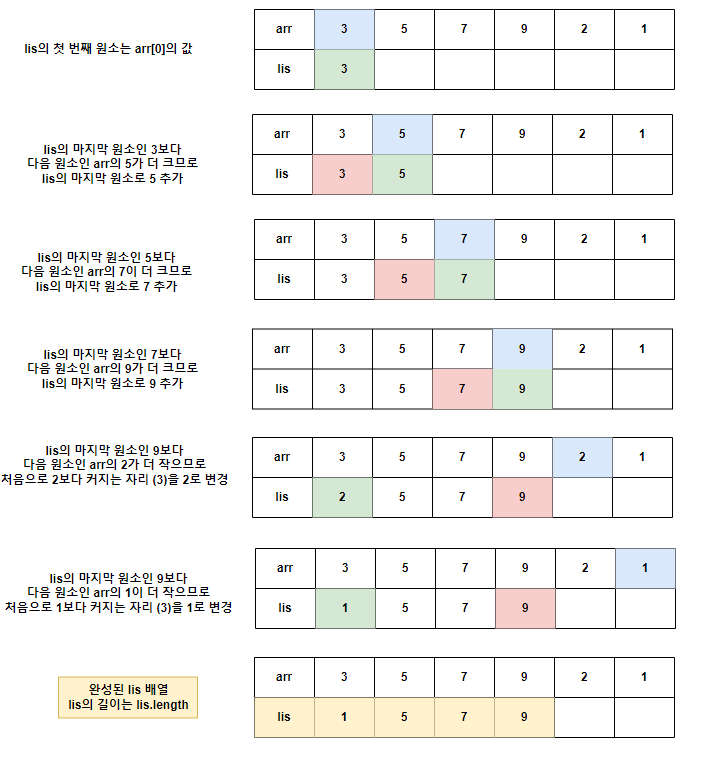
이 방법을 이용하면 증가하는 부분수열의 최장길이를 \(O(N{log}N) = 6 * 10^6\), 즉 1초 미만으로도 쉽게 구할 수 있는데 이때 list에 들어있는 값들이 LIS에 해당하는 원소들이라는 것을 보장할 수 없다. 백준 14003번 문제는 LIS에 해당하는 원소들도 같이 출력해주어야 해서 위 방법을 조금 변형해서 적용해주었다.

이분탐색 Collections.BinarySearch()

아, 이분탐색할 때는 내장 함수 Collections.BinarySearch() 를 이용하면 편리하다. 해당 값이 list에 존재하지 않을 경우에는 - (원래라면 들어갔어야 할 index + 1) 를 반환해주니 해당 부분 처리만 해주면 끝!

🖤 How?

어떻게 하냐면…!
또 새로운 배열에 idx에 그 수(값)을 저장해주는 것이 아니라 LIS 배열에서의 인덱스를 저장한다. 일단 LIS의 최장길이는 list의 최종 길이가 되고, LIS에 해당하는 원소들은 뒤에서부터 역추적해나간다.

idx의 끝에서부터 출발해서 값이 list의 최종 길이 - 1인 것부터 하나씩 줄여나가면서 해당하는 원소를 찾을 수 있다. 코드로는 다음과 같다.

int now = list.size();
int[] ans = new int[now];

for (int i=N-1, x=list.size()-1; i>=0; i--) {
     if (now == idx[i]+1) {
          ans[x--] = A[i];
          now --;
     }
}

내가 이해한 개념을 간단하게 정리하려고 적었지만 혹시나 이 글을 보는 누군가도 이해가 잘 되었길 바라며, 성공한 최종 코드는 아래에 첨부해놓았다.

혹시나 해서 내가 이해할 때 도움이 되었던 블로그도 가져왔다! 그림이 알기 쉽게 설명되어 있다.
(이 링크에 있는 LIS 구현 코드는 잘 작동하지 않으니 주의하길.. 구현 코드는 아래 최종코드 참고하시면 될 것 같습니다.)

💻 내 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class Main {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int N = Integer.parseInt(br.readLine());
		int[] A = new int[N];
		A = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();

		List<Integer> list = new ArrayList<>();
		int[] idx = new int[N];

		for (int i=0; i<N; i++) {
			int pos = Collections.binarySearch(list, A[i]);
			if (pos < 0)
				pos = - (pos + 1);
			idx[i] = pos;
			if (pos == list.size()) list.add(A[i]);
			else list.set(pos, A[i]);
		}
		System.out.println(list.size());
		int now = list.size();
		int[] ans = new int[now];

		for (int i=N-1, x=list.size()-1; i>=0; i--) {
			if (now == idx[i]+1) {
				ans[x--] = A[i];
				now --;
			}
		}
		for (int a: ans) sb.append(a +" ");
		System.out.println(sb);
	}
}