TIL | Logistic Regression |
[ AI / ML ] 로지스틱 회귀
👩🏻💻 K-MOOC 실습으로 배우는 머신러닝 강의
📙 해당 포스트는 K-MOOC 강의 내용과 추가로 다른 자료들을 찾아 내용을 작성하였으며, 이론 및 개념에 대해 공부하고 예제 실습도 진행한 후 내용을 정리하였다.
Logistic Regression
로지스틱 회귀는 이름에 회귀가 들어가지만 분류 Classification 작업에 사용할 수 있다.
이진 분류 Binary Classification
컴퓨터공학과 학생들이 중간고사로 알고리즘 시험을 봤다고 가정을 해보자. 이때 Pass와 Fail로 성적이 나뉘는데, 그 커트라인은 공개되지 않았다. 이때, 로지스틱 회귀를 이용해서 넘겨받은 학생들의 데이터로부터 특정 점수를 얻었을 때 Pass와 Fail을 판정하는 모델을 만들 수 있다.
해당 내용을 선형으로 나타내면 분류 작업이 잘 작동하지 않는다. 로지스틱 회귀는 S자 모양의 그래프를 만들어서 분류 예측 작업을 진행한다. S자 모양의 그래프로 만들어 줄 수 있는 함수 중 하나인 시그모이드에 대해 알아보자.
Sigmoid 함수
선형 회귀와 마찬가지로 로지스틱 회귀 역시 최적의 W와 b를 찾는 것이 목표이다.
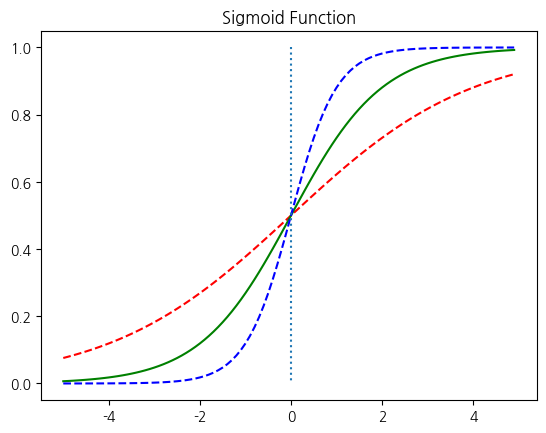
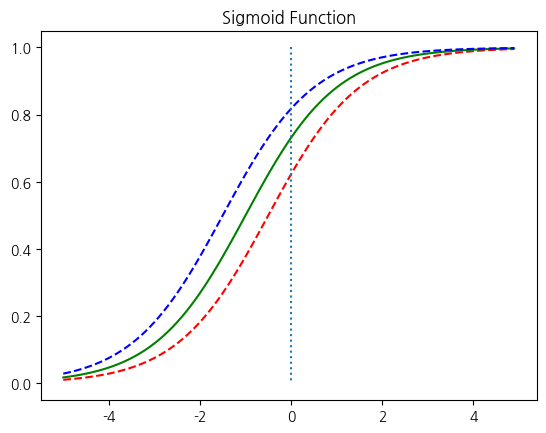
시그모이드 함수는 입력값이 한없이 커지면 1에 수렴하고, 입력값이 한없이 작아지면 0에 수렴한다. 시그모이드 함수의 출력값은 0과 1 사이의 값을 가지는데 이 특성을 이용하여 분류 작업에 사용할 수 있다. 출력값을 확률이라고 생각을 하면 해당 레이블에 속할 확률이 50%가 넘으면 해당 레이블로 판단하고, 해당 레이블에 속할 확률이 50%보다 낮으면 아니라고 판단하는 것으로 볼 수 있다. 이와 마찬가지로 multi-class classification도 로지스틱 회귀를 이용해 수행할 수 있다.
비용 함수 Cost Function
이제 아래의 가설에서 최적의 W와 b를 찾을 수 있는 cost function을 정의해야 한다.
[ 로지스틱 회귀 가설 ]
🤔 선형 회귀와 로지스틱 회귀의 cost function?
➡️ 선형 회귀에서 사용했던 cost function 평균 제곱 오차 MSE : Mean Squared Error를 로지스틱 회귀의 cost function으로 사용하면 안될까?
다음은 선형 회귀에서 사용했던 MSE의 수식이다.
[ Mean Squared Error ]
위의 cost function 수식에 로지스틱 회귀의 가설을 대입하고 미분하면 심한 비볼록 (non-convex) 형태의 그래프가 나온다.
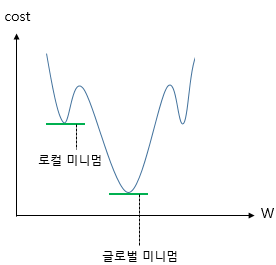
위와 같은 그래프는 경사 하강법을 사용했을 때 Local minimum을 Global minimum 값이라고 착각해서 최적의 가중치 W가 아닌 다른 값을 택하면 모델의 성능이 낮게 나올 수 있다. cost가 최소가 되는 가중치 W를 찾은 것이 아니기 때문에 cost function의 목적에 맞지 않다.
시그모이드 함수는 0과 1 사이의 값을 출력한다. 실제값이 1일 때 예측값이 0에 가까워지면 오차가 커져야 하고, 실제값이 0일 때 예측값이 1에 가까워지면 오차가 커져야 한다. 이를 충족시키는 함수가 바로 로그 함수이다. 이를 이용해 cost function을 지정해줄 수 있다.
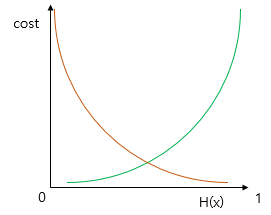
이를 식으로 나타내면
로 나타낼 수 있다. 그럼 이 두 수식을 하나의 수식으로 통합해보자.
[ 로지스틱 회귀 Cost Function ]
위의 cost function에 대해 경사 하강법을 수행하면서 최적의 가중치 W를 찾는다. 이를 수식으로 나타내면 다음과 같다.
[ 최적의 W 구하기 ]
💻 실습 예제 코드
PyTorch로 로지스트 회귀 구현하기
[ 필요한 도구 import ]
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
[ W와 b 값 초기화 ]
W와 b를 전부 0으로 초기화해주자.
W = torch.zeros((2, 1), requires_grad=True) # 크기는 2 x 1
b = torch.zeros(1, requires_grad=True)
W와 b를 전부 0으로 초기화해준 상태에서 예측하면 예측값은 전부 0.5가 나온다.
# hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis) # 예측값인 H(x) 출력
tensor([[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000]], grad_fn=<MulBackward>)
[ 모델 훈련 ]
이제 모델을 훈련해보자.
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
# cost = -(y_train * torch.log(hypothesis) +
# (1 - y_train) * torch.log(1 - hypothesis)).mean()
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
Epoch 0/1000 Cost: 0.693147
... 중략 ...
Epoch 1000/1000 Cost: 0.019852
위의 코드에서는 직접 벡터 계산을 한 후에 torch의 Sigmoid 함수를 적용해줬지만 아래 코드처럼 nn.Module을 이용해서 한 번에 연결해서 계산할 수도 있다. 난 이 방법이 더 간단하고 나중에 layer을 쌓기도 편해서 nn.Module을 많이 쓴다. 그리고 뒤에 인공 신경망을 더 배우면서 나오겠지만, 시그모이드 함수는 인공 신경망의 은닉층에서는 거의 사용되지 않는다.
model = nn.Sequential(
nn.Linear(2, 1), # input_dim = 2, output_dim = 1
nn.Sigmoid() # 출력은 시그모이드 함수를 거친다
)
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = model(x_train)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 10 == 0:
prediction = hypothesis >= torch.FloatTensor([0.5]) # 예측값이 0.5를 넘으면 True로 간주
correct_prediction = prediction.float() == y_train # 실제값과 일치하는 경우만 True로 간주
accuracy = correct_prediction.sum().item() / len(correct_prediction) # 정확도를 계산
print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format( # 각 에포크마다 정확도를 출력
epoch, nb_epochs, cost.item(), accuracy * 100,
))
[ 예측 ]
학습 끝! 학습 후 최적의 W와 b를 가지고 예측값을 구해보자.
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis)
tensor([[2.7648e-04],
[3.1608e-02],
[3.8977e-02],
[9.5622e-01],
[9.9823e-01],
[9.9969e-01]], grad_fn=<SigmoidBackward>)
마지막으로, test data에 대해서 예측까지!!
prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction)
다음 포스트에서 만나요 🙌
참고
Related Posts
| TIL | LeakGAN이란? - NLP Text Generation Model | |
| TIL | GAN - NLP Text Generation Model | |
|
TIL | Clustering Code | 군집화 실습 코드 |
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).