[ AI / ML / DL ] Neural Networks Basic - Basic Structure, Multi-layered Structure
👩🏻💻 K-MOOC 실습으로 배우는 머신러닝 강의
📙 해당 포스트는 K-MOOC 강의 내용과 추가로 다른 자료들을 찾아 내용을 작성하였으며, 이론 및 개념에 대해 공부하고 예제 실습도 진행한 후 내용을 정리하였다.
1. Basic Structure
로지스틱 회귀는 인공 신경망을 이루는 하나의 perceptron에 해당한다고 볼 수 있다.
🤔 퍼셉트론이란
딥 러닝을 이해하기 위해서는 우선 인공 신경망에 대한 이해가 필요한데, 퍼셉트론(Perceptron)이 바로 초기의 인공 신경망이다.
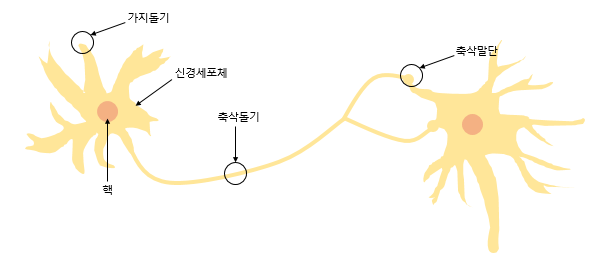
퍼셉트론은 실제 뇌를 구성하는 신경 세포 뉴런의 동작과 유사하다. 뉴런은 가지돌기에서 신호를 받아들이고, 이 신호가 일정치 이상의 크기를 가지면 축삭돌기를 통해서 신호를 전달한다.
x는 입력값을 의미하며, W는 가중치(Weight), y는 출력값입니다. 그림 안의 원은 인공 뉴런에 해당됩니다. 실제 신경 세포 뉴런에서의 신호를 전달하는 축삭돌기의 역할을 퍼셉트론에서는 가중치가 대신합니다. 각각의 인공 뉴런에서 보내진 입력값 는 각각의 가중치 와 함께 종착지인 인공 뉴런에 전달된다.
2. Multi-layered Structure
활성화 함수 Activation Functions
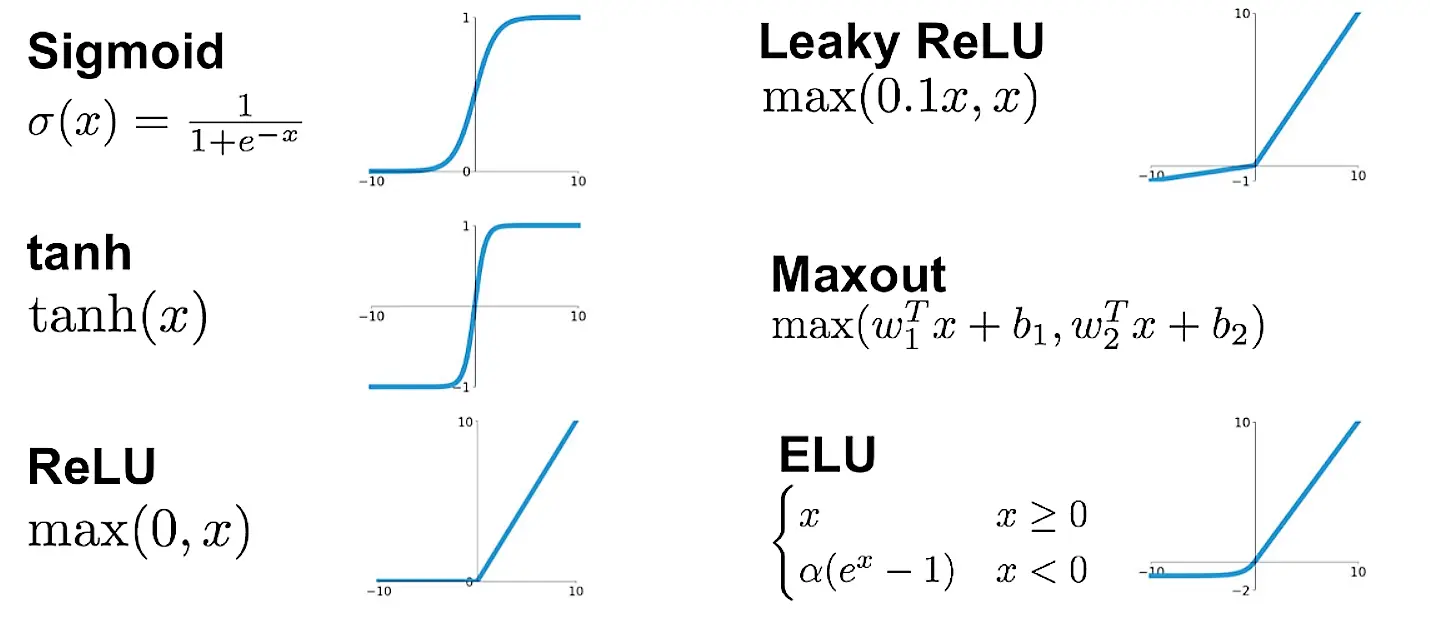
1. 비선형 함수 Nonlinear Functions
비선형 활성화 함수(Activation function)는 입력을 받아 수학적 변환을 수행하고 출력을 생성하는 함수이다.
인공 신경망의 능력을 높이기 위해서는 은닉층을 여러 개 추가해야 한다. 그런데 만약 활성화 함수로 선형 함수를 사용하게 되면 은닉층을 쌓을 수가 없다. 활성화 함수로 선형 함수를 선택하고 은닉층을 계속 쌓아도 은닉층을 1회 추가한 것과 동일한 효과를 주기 때문이다.
➕ 선형 함수를 사용한 것이 아무 의미가 없는 것은 아니고, 학습 가능한 가중치가 새로 생긴다는 점에서 의미가 있긴 하다. 이에 선형 함수를 사용한 층을 활성화 함수를 사용하는 은닉층과 구분하기 위해 선형층 (linear layer) 이나 투사층 (projection layer) 등의 다른 표현을 사용하여 표현하기도 한다.
2. 시그모이드 함수와 기울기 소실
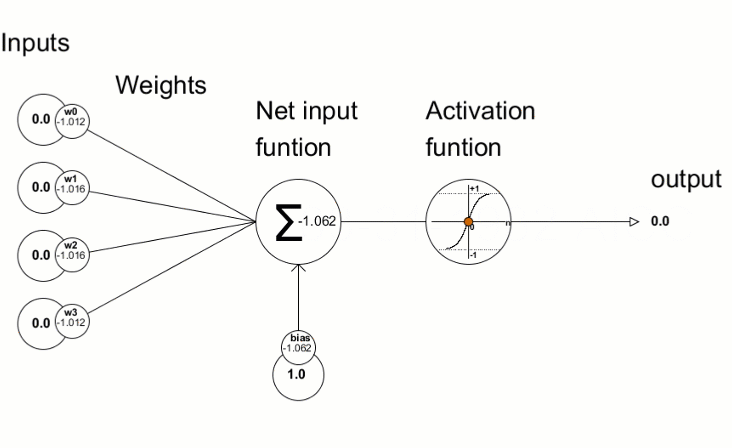
위 인공 신경망의 학습 과정은 다음과 같다.
우선 인공 신경망은 입력에 대해서 순전파(forward propagation) 연산을 하고, 그리고 순전파 연산을 통해 나온 예측값과 실제값의 오차를 손실 함수(loss function)을 통해 계산하고, 그리고 이 손실(loss)을 미분을 통해서 기울기(gradient)를 구하고, 이를 통해 역전파(back propagation)를 수행한다.
역전파 과정에서 0에 가까운 아주 작은 기울기가 곱해지게 되면, 앞단에는 기울기가 잘 전달되지 않게 됩니다. 이러한 현상을 기울기 소실(Vanishing Gradient) 문제라고 한다.
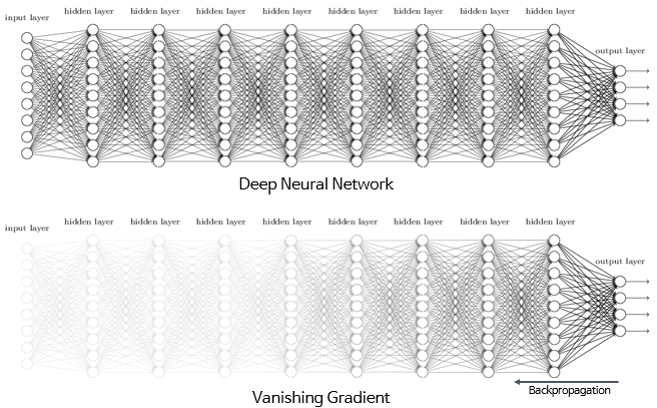
시그모이드 함수를 사용하는 은닉층을 여러 개 쌓게 되면 0에 가까운 기울기가 계속 곱해지면 앞단에서는 거의 기울기를 전파받을 수 없게 된다. 다시 말해 매개변수 W가 업데이트 되지 않아 학습이 되지 않는다.
➡️ 시그모이드 함수를 은닉층에서 사용하는 것 지양 ❌
3. tanh 함수
하이퍼볼릭탄젠트 함수(Hyperbolic tangent function)는 입력값을 -1과 1 사이의 값으로 변환한다.
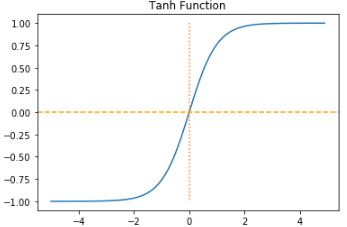
tanh 함수는 시그모이드 함수와는 달리 0을 중심으로 하고 있는데, 이때문에 시그모이드 함수와 비교하면 반환값의 변화폭이 더 크다. 그래서 시그모이드 함수보다는 기울기 소실 증상이 적은 편입니다. 그래서 은닉층에서 시그모이드 함수보다는 많이 사용되는 편이다.
4. ReLU 함수
인공 신경망에서 가장 최고의 인기를 얻고 있는 함수로, 수식은 다음과 같다.
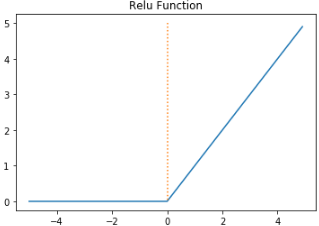
ReLU 함수는 특정 양수값에 수렴하지 않으므로 깊은 신경망에서 시그모이드 함수보다 훨씬 더 잘 작동한다. ReLU 함수는 시그모이드 함수와 tanh 함수와 같이 어떤 연산이 필요한 것이 아니라 단순 임계값이므로 연산 속도도 빠르다.
그러나 ReLU 함수도 문제점을 가지고 있다. 입력값이 음수면 기울기도 0이 된다. 그리고 이 뉴런을 다시 회생시키는 것이 매우 어렵다. 이 문제를 죽은 렐루(dying ReLU)라고 한다. 그래서 제안된 함수가 Leaky ReLU이다.
5. Leaky ReLU
dying ReLU 문제를 보완하기 위해 ReLU의 변형 함수들이 등장하기 시작했다. 그 중 하나가 Leaky ReLU이다. Leaky ReLU는 입력값이 음수일 경우에 0이 아니라 0.001과 같은 매우 작은 수를 반환하도록 되어있다. 수식은 다음과 같다.
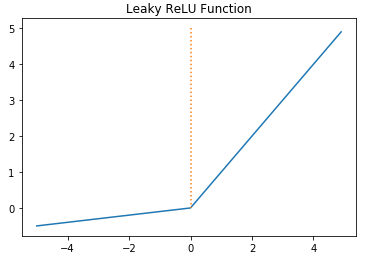
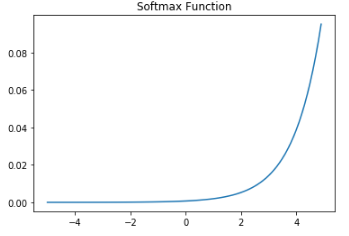
6. Softmax function
multi-class classification을 할 때 주로 사용했던 Softmax 함수를 출력층에 적용하여 분류 문제를 예측한다.
7. 출력층의 활성화 함수와 오차 함수의 관계
다음은 각 문제에 따른 출력층의 활성화 함수와 비용 함수의 관계이다.
| 문제 | 활성화 함수 | 비용 함수 |
|---|---|---|
| 이진 분류 | Sigmoid | nn.BCELoss() |
| 다중 클래스 분류 | Softmax | nn.CrossEntropyLoss() |
| 회귀 | 없음 | MSE |
✅ 주의할 점 : nn.CrossEntropyLoss()는 Softmax 함수를 이미 포함하고 있다.
스탠포드 대학교의 딥 러닝 강의 cs231n에서는 ReLU를 먼저 시도해보고, 그다음으로 LeakyReLU나 ELU 같은 ReLU의 변형들을 시도해보며, sigmoid는 사용하지 말라고 권장합니다.
💻 실습 예제 코드
다층 퍼셉트론으로 손글씨 분류하기
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt # 시각화를 위한 맷플롯립
%matplotlib inline
digits = load_digits() # 1,979개의 이미지 데이터 로드
images_and_labels = list(zip(digits.images, digits.target))
for index, (image, label) in enumerate(images_and_labels[:5]): # 5개의 샘플만 출력
plt.subplot(2, 5, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('sample: %i' % label)

X = digits.data # 이미지. 즉, 특성 행렬
Y = digits.target # 각 이미지에 대한 레이블
import torch
import torch.nn as nn
from torch import optim
model = nn.Sequential(
nn.Linear(64, 32), # input_layer = 64, hidden_layer1 = 32
nn.ReLU(),
nn.Linear(32, 16), # hidden_layer2 = 32, hidden_layer3 = 16
nn.ReLU(),
nn.Linear(16, 10) # hidden_layer3 = 16, output_layer = 10
)
X = torch.tensor(X, dtype=torch.float32)
Y = torch.tensor(Y, dtype=torch.int64)
loss_fn = nn.CrossEntropyLoss() # 이 비용 함수는 소프트맥스 함수를 포함하고 있음.
optimizer = optim.Adam(model.parameters())
losses = []
for epoch in range(100):
optimizer.zero_grad()
y_pred = model(X) # forwar 연산
loss = loss_fn(y_pred, Y)
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, 100, loss.item()
))
losses.append(loss.item())
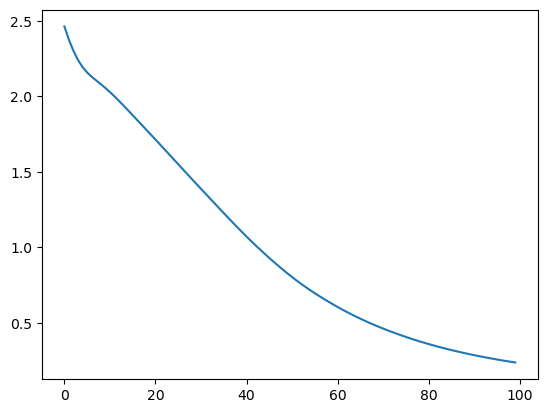
plt.plot(losses)
Epoch 0/100 Cost: 2.380815
Epoch 10/100 Cost: 2.059323
... 중략 ...
Epoch 90/100 Cost: 0.205398
마무리하면서..
다음 포스트에서 만나요 🙌
참고
Related Posts
| AI | LLM(Large Language Model)은 어떻게 답변을 생성하는 걸까? | |
| AI | 트랜스포머(Transformer) 쉽게 이해하기 | |
| 빅데이터 | 특성 추출 Feature Extraction |
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).