[ 빅데이터 ] 특성 추출 Feature Extraction - PCA / t-SNE / LDA
일반적으로 데이터가 많으면 모델의 성능이 더 향상된다. 그러나 실제 데이터셋은 불필요한 정보를 포함하고 있거나, 유사한 의미를 가지고 있지만 여러 feature로 나눠져 있는 경우가 많다. 그만큼 많은 시간이 소요되기 때문에 데이터 feature 를 적당히 줄여주는 작업도 필요하다. feature 를 줄이는 방법에는 크게 Feature Selection 과 Feature Extraction 방법으로 나눌 수 있다. 지난 번 Feature Selection에 이어 Feature Extraction에 대해 알아보자.
지난 포스트
[ 빅데이터 ] 특성 선택 Feature Selection - Filter / Wrapper / Embedded
[ 빅데이터 ] 차원의 저주 (The curse of dimensionality) 란?
특성 추출 Feature Extraction 이란?
기존 feature 들의 조합으로 유용한 feature 를 새롭게 생성하는 방법
Feature Extraction은 고차원의 원본 feature 공간을 저차원의 새로운 feature 공간으로 투영한 방법이다. 특성들 사이에 특성이나 관계를 잘 표현할 수 있는 새로운 선형/비선형 결합 변수를 만들어 데이터를 줄인다.
⭐️⭐️ 이로 인한 효과는 다음과 같다.
- feature 개수 많이 줄일 수 있음
- feature 간 상관관계 고려 용이
단, 이렇게 추출된 변수의 해석이 어렵다는 단점이 있다.
Methods
1️⃣ 주성분 분석 PCA
일반적으로 차원을 축소할 때 주성분 분석 (PCA) 을 주로 사용한다.
💡 원리
- 데이터에 가장 가까운 초평면을 정의
- 이 평면에 데이터를 투영시킨다.
- train set에서 분산이 최대인 축을 찾는다.
❓ 분산이 최대인 축을 찾는 이유
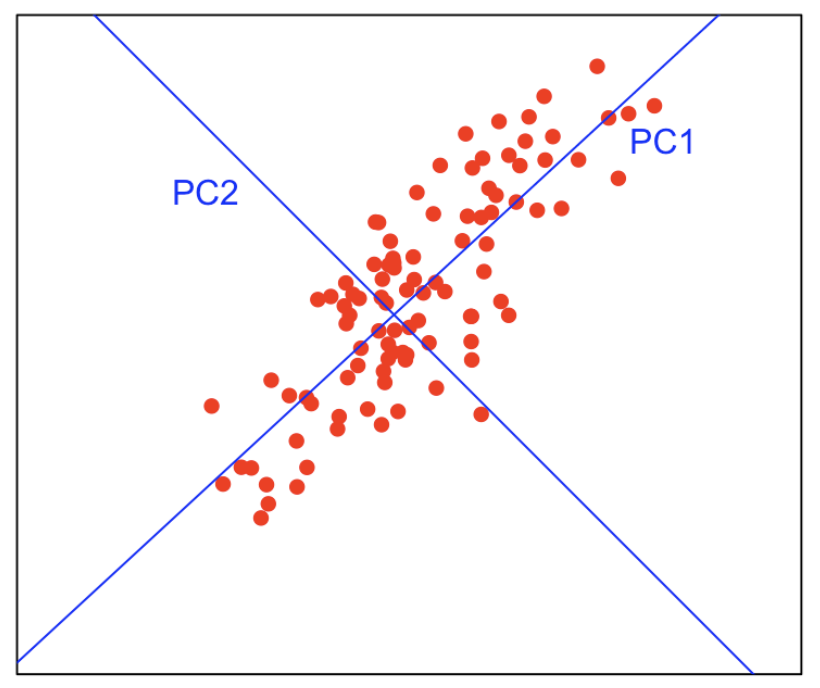
분산이 큰 축일수록 더 많은 정보를 가지고 있다.
즉, 이 말은 원본 데이터를 최대한 보존하기 떄문에 원본 위치 정보를 더 잘 복원할 수 있다는 말이 된다. 최대한 정보 손실을 줄이기 위해 분산이 최대인 축을 찾아서 차원 축소를 진행한다. 위 그림의 경우 분산이 더 큰 PC2를 축으로 하는 것이 좋다.
그럼에도 불구하고, 선형 분석 방식으로 투영하기 때문에 차원이 감소되면서 데이터들이 뭉개져 군집 또한 변별력을 잃을 수 있다.
2️⃣ t-SNE
PCA는 선형 차원 축소 기법으로, PCA 분석을 통해 차원을 줄이는 과정에서 군집의 변별력이 사라지는 경우가 있다. 이러한 문제를 해결할 수 있는 차원 감소 방법으로 t-SNE 방식을 사용한다.
t-SNE는 비선형 차원 축소 기법으로, 대략적인 원리는 다음과 같다.
💡 원리
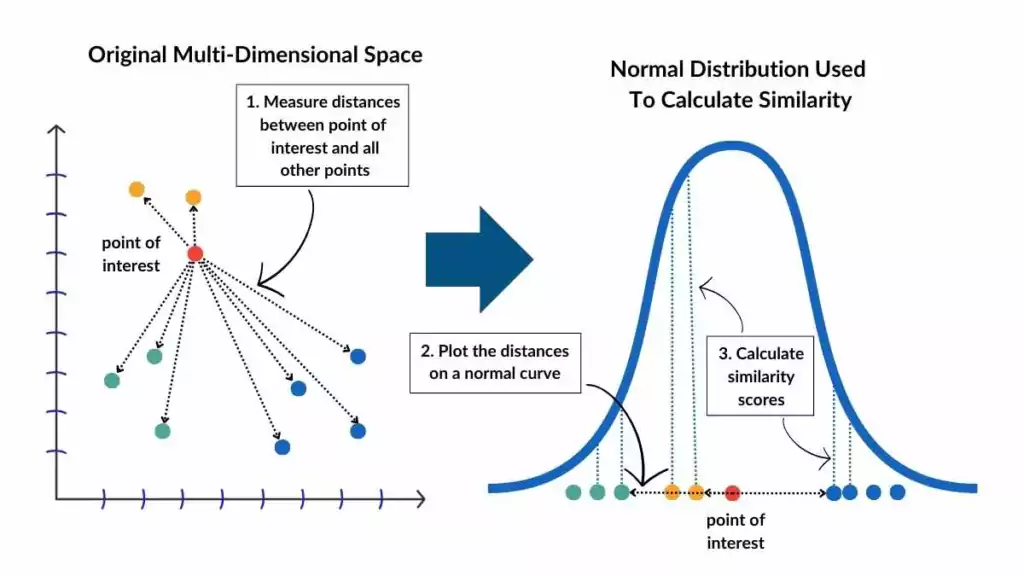
- 임의의 점(A)을 하나 선택해 다른 점(B)까지의 거리를 측정한다.
- 점 A 를 T 분포 그래프 가운데 위치시킨다.
- A 로부터 B 까지 거리에 있는 T 분포 값을
친밀도 similarity라고 하고, 친밀도가 가까운 값끼리 묶는다.
💡 장점 & 단점
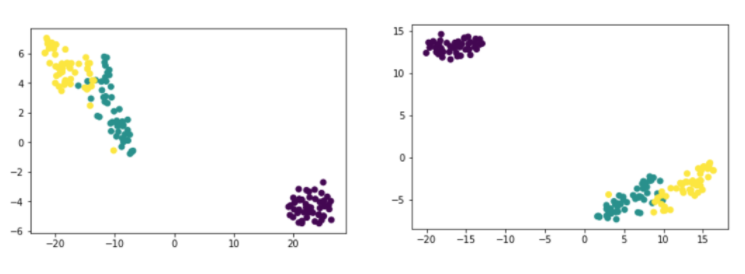
- 군집이 뭉개지는 PCA 의 단점을 해결
- 매번 계산할 때마다 축의 위치가 바뀌어 다른 모양으로 나타남
- 데이터의 군집성과 같은 특성은 유지가 되어 시각화를 통한 데이터 분석에서는 유용
- 특성 값이 매번 바뀌기 때문에 머신러닝 모델의 학습 feature 로 사용되기에는 다소 어려움
3️⃣ LDA
LDA 도 PCA와 마찬가지로 선형 판별 분석법으로 매우 유사하다. 데이터를 저차원 공간에 투영해 차원을 축소하는 방법으로, PCA와 달리 지도학습 분류 문제에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소한다. 그리고 PCA와 달리 LDA는 지도학습이기 때문에 target 값을 넣어줘야 한다.
그래서 PCA 는 입력 데이터의 분산이 가장 큰 축을 찾았지만, LDA 는 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾는다.
클래스 간 분산은 최대화, 클래스 내부 분산은 최소화
💡 활용 분야
LDA의 이러한 특성 때문에 토픽모델링 태스크에서도 활용되었었다. LDA 는 특정 토픽에 특정 단어가 나타날 확률을 계산해준다.
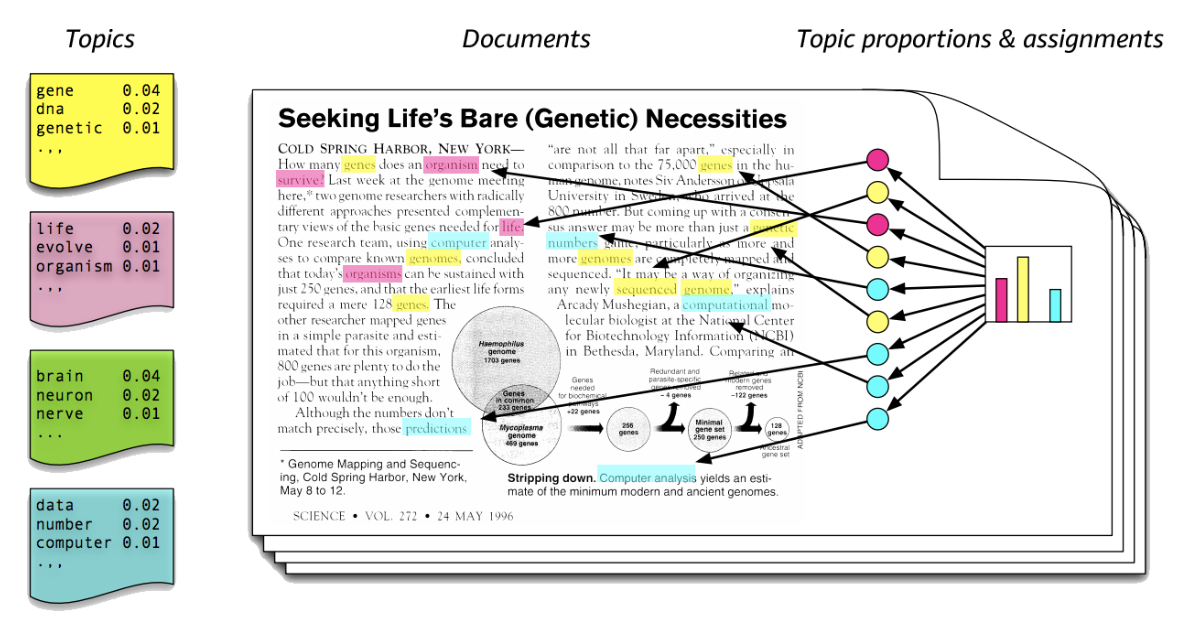
위의 그림을 예시로 들어보자면, 노란색 토픽은 gene, dna, genetic 이라는 단어가 나올 확률이 높은 걸로 보아 유전자 관련 주제일 것이다. 한편, 문서를 보면 빨간색, 파란색 토픽에 해당하는 단어보다 노란색 토픽에 해당하는 단어가 더 많은 걸로 보아 노란색 토픽일 가능성이 높을 것이다. 이런식으로 LDA를 이용해 문서의 토픽을 추출해낸다. 현재는 물론 LLM이 성능이 훨씬 뛰어나다!
📍 더 자세히 보러가기
LDA란? - NLP Topic Modeling
Reference
Related Posts
| AI | LLM(Large Language Model)은 어떻게 답변을 생성하는 걸까? | |
| AI | 트랜스포머(Transformer) 쉽게 이해하기 | |
| 빅데이터 | 특성 선택 Feature Selection |
💙 You need to log in to GitHub to write comments. 💙
If you can't see comments, please refresh page(F5).